Алгоритм Евклида
Если хотите быстро ознакомится только с содержанием статей, смотрите ниже.
Текст, для быстрого ознакомления (в тексте для быстрого ознакомления формулы могут отображаться не корректно):
Страница переведена на новый сайт https://myeducation.su/ : страница
ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЖУРНАЛ Квант (6 июнь 1972)
Для того, чтобы найти НОД двух
чисел, можно, конечно, действовать
так: выписать все делители каждого
из чисел, выбрать общие делители,
а затем взять из них наибольший.
Можно поступить иначе, не отыскивая
отдельно делители каждого из чисел.
Докажем следующую важную
лемму.
Лемма 1. Пусть а = bq -r,
тогда НОД (а, Ь) = НОД (Ь, г).
С этой целью покажем, что у пары
чисел (а, Ь) множество общих дели-
телей в точности такое же, как у пары
чисел (Ь, г). Отсюда, конечно, будет
следовать, что и НОД у этих пар один
и тот же. Итак, докажем, что каждый
общий делитель чисел а и Ь является
также делителем числа г, и наоборот,
что каждый общий делитель чисел Ъ
и г является делителем числа а.
Докажем сначала первое утверж-
дение. Пусть а и b делятся на k.
Тогда bq делится на k (см. 2 из
п. 1) и г = а — bq делится па к
(см. 1 из п. I).
Перейдем ко второму утвержде-
нию. Если b и г делятся на ;/ц то
bq делится на т и а — bq + г де-
лится на т (здесь мы опять пользо-
вались утверждениями 1 и 2 из
п. I).
Доказанная лемма позволяет лег-
ко и быстро находить НОД двух чи-
сел. Посмотрим, как это делается.
Пример. Найдем, чему равен
НОД F069, 663).
Р е ш е и и с. Разделим 6069 на
663 с остатком:
6069 = 663-9 — 102.
Из леммы следует, что
НОД F069, 663) — НОД F63, 102).
Ищем НОД F63, 102). Для этого
делим 663 на 102:
663 = 102-6 4-51.
Снова, применив лемму, получаем
НОД F63, 102) НОД A02, 51).
Но 102 делится на 51 без остатка:
102 = 51-2,
поэтому НОД A02, 51) = 51, сле-
довательно,
51 = НОД A02, 51)
ПОД F63, 102) = НОД F069, 663).
Отпе т. НОД F069, 663) =- 51.
•Метод отыскания наибольшего об-
щего делителя, основанный на по-
следовательном применении леммы 1,
носит специальное название — ал-
горитм Евклида.
Задача 13. Найдите наибольший
Общий делитель чисел:
я) 987 654 321 и 123 456 789,
6) 7 777 777 777 к 777 777.
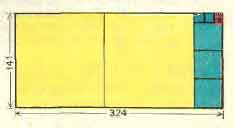
Задача 14. От прямоугольника
324 си х 141 см отрезают несколько квадра-
тов со стороной 141 см, пока lie останется
прямоугольник, у которого одна из сторон
Рис. 3.
меньше 141 см. От полученного прямоуголь-
ника снова отрезают квадраты, стороны ко-
торых равны его меньший стороне, до тех
пор. пока это возможно, и гак далее (рис. 3).
На какие квадраты будет разрезан пря-
моугольник? (Укажите их размеры и колн-
Итак, алгоритм Евклида — это
простой метод нахождения наиболь-
шего общего делителя двух чисел.
Если у нас имеется два числа а и Ь,
причем а > b > 0, то сначала де-
лим а на b п получаем остаток г,,
который меньше, чем Ь. Затем мы
делим число b на г, и находим ос-
таток г.,, который меньше, чем г,.
Далее, мы делим число гЛ па число
г.,, при этом получаем остаток гг,
меньший, чем г.,, и так далее, пока
какой-нибудь остаток rn_Y не раз-
делится на остаток г„ нацело, без
остатка (то есть г,,^! 0).
Ясно, что указанный процесс обя-
зательно кончится, поскольку каж-
дый остаток меньше предыдущего, а
32 Алгоритм Евклида
Рис. 4. Пусть а н b — два отрезка, а ~> Ь.
Отложим Ь на а столько раз, сколько воз-
можно получим остаток г,. Отложим тх на b
столько раз, сколько возможно; получим ос-
таток г2. Отложим гг на г, сколько воз-
можно; получим остаток г3, и т. д.
Если, откладывая некоторое тп на /¦„_,,
мы не получим остатка (то есть гл + | 0),
то отрезок гп и есть наибольшая общая
мера отрезков я и Ь Если длины а и b —
целые, то все остатки rt, r4,… также имеют
целые длины, процесс откладывания обор-
вется и последнее тп и есть НОД (а, Ь). Если
процесс откладывания отрезков не обры-
вается, то отрезки аи несоизмеримы
(отношение иррационально).
вес остатки — неотрицательные чис-
ла. Последний остаток гп и есть
НОЛ (а, Ь):
г„ — НОД (г,„ г„_,) —=
ПОД (/-„.г. г„_2) . ..=
= НОД(г., г,)-НОД (г,, Ь) =
НОД (я, Ь).
С одной геометрической иллюст-
рацией алгоритма Евклида мы встре-
тились в задаче 14. Более известный
к важный геометрический вариант
алгоритма Евклида — алгоритм отыс-
кания наибольшей общей меры двух
отрезков (рис. 4).
Задача 15. Найдите наибольшее чне-
15 6
ло а. такое, что числа -ттгг и «og^»—полно.
Другими словами, найдите длину отрезка а.
являющегося наибольшей bfiua-.ii мерой от-
реякоп длиной —. и -1 .
33 Алгоритм Евклида