§ 4. Динамика прямолинейного движения.
Страницы переведены на новый сайт:
СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ
https://myeducation.su/sbornik-zadach-po-elementarnoj-fizike/
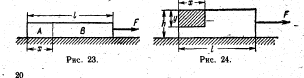
Однородный брусок, масса которого М , движется
ускоренно под действием силы F по гладкой поверхности.
Найти величину Т силы, с которой часть бруска А длины х
действует на часть бруска В. Длина бруска /. (Рис. 23.)
й-вием силы Т7. Масса бруска М. Определить силы, дейст-
— вующие на заштрихованную часть бруска. Линейные размеры
указаны на рис. 24. Трением пренебречь.
75. На однородный стержень длины L действуют две
‘ силы./7! и F2, приложенные к его концам и направленные в
Противоположные стороны (рис. 25). С какой силой F
20 Динамика прямолинейного движения.
растянут стержень в сечении, находящемся на расстоянии
Т от одного из его концов? ‘
76. Брусок массы т лежит на полу лифта. Лифт движется
с ускорением а, направленным вниз. Определить
силу, с которой брусок действует на пол лифта. При каком
ускорении лифта исчезают деформации в бруске? С какой ,
сйлой брусок будет действовать на пол лифта, если лифт начнет
двираться с ускорением а, направленным вверх?
77. Мальчик массы 44 бежит вверх по неподвижной доске
массы т, находящейся на наклонной плоскости с углом
при основании а. Трение между доской и плоскостью отсутствует.
Какой путь прошел мальчик к моменту, когда
его скорость, равная вначале и0. ‘уменьшилась в 2 раза,
оставаясь той же по направлению? ’
78. Однородный брусок висит на нити; Нить разрезают.
У каких частиц бруска будет большее ускорение в
начальный момент времени: у верхних или у нижних?.
79. Однородный брусок лежит на горизонтальной подставке.
Подставку внезапно убирают. У каких частиц брус-
„ка будет большее ускорение в начальный момент времени:
у верхних или у нижних?
86. Человек е поднятыми руками стоит на платформе
-медицинских весов. Как изменяются показания весов при
ускоренном движении рук вниз? — ‘
81. На одной’ чашке весов находится бутылка. В бутылке
— муха. Пока муха спит, весы уравновешены. Нарушится
ли равновесие весов, когда проснувшаяся муха,
оторвется от стенки бутылки и полетит сначала в горизонтальном
направлении, а затем вверх с ускорением а?
21 Динамика прямолинейного движения.
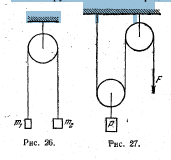
82. На крицах ним, перекинутой через -блок с неподвижной
осью, висят на высоте Н—2 м от нола два груза,
массы которых т ,.= 100 г и т 2=2О0 г (рис. 26). В начальный
момент грузы покоятся. Определить натяжение нити при
ш р ш ш ш щ движении грузов ивре-
>^\\\\\\^ ] “ мя, за которое груз массы
тг достигнет шла.
Массу блока и нити не
учитывать.
83. К оси подвижного
блока прикреплен
груз весом Р (рис, 27).
С какой силой F нужно
тянуть конец нити, перекинутой
через второй
блок, чтобы груз Р
двигался вверх с ускорением
а? Чтобы груз
покоился? Массой блоков
и нити пренебречь.
84. Определить ускорения г р у з » с массами ты -т„
та, а также натяжение нитей в системе, изображенной
на рис. 28; если m1=m2+m 3. Массы нитей и блоков ничтожно
малы по сравнению с массами грузов.
85. Через. два неподвижных блока перекинута нить,
к концам которой подвешены чашки с гирями весом по Р —
=30 Н на каждой. Нить между блоками разрезали и присоединили
jn динамометру (ряс. 29). Что покажет динамометр?
22 Динамика прямолинейного движения.
Какой груз P i нужно добавить на одну из чашек для того,
чтобы показание динамометра не изменилось после того,
как с другой чашки была снята гиря, весом Р 2=10 Н?
Массами чашек, блоков, нити и динамометра пренебречь.
86. На нити, перекинутой через блок, подвешены грузы
с массами т± и тг. Блок в заторможенном состоянии
(грузы не движутся) уравновешен на рычажных весах,
как показано на рис. 30. На сколько придется изменить вес
гирь на правой чашке, чтобы при освобождении блока
и последующем движении грузов равновесие сохранилось?
№
к у
№
Рис. 31.
ш ж ш ж
г л В
87. Система состоит из двух блоков с неподвижными
осями и одного подвижного (рис. 3’1)!. Через блоки перекинута
нить, на концах которой подвешены
грузы с массами mL и та, а к
оси подвижного блока .подвешен груз
с массой тг. Участки нити, не лежащие
на блоках, вертикальны. Определить
ускорение каждого из грузов, если
массами блоков и нитей, а также трением
можно пренебречь.
88. Определить ускорения грузов в
системе, изображенной на рис. 32. Массами
блоков, нити и трением пренебречь.
В какую сторону будут вращаться блоки
при движении грузов?
89. Определить натяжения нитей,
на которых висят грузы в системе, изображенной
на рис. 33. Массой нитей и
блоков пренебречь. Трение отсутствует.
Массы грузов т.и тг, тг, т4, т6„ mt,
m,, mt известны.
23 Динамика прямолинейного движения.
90. Определить ускорение груза массы от * системе,
изображенной на рис. 34. Массой нитей . и Шоке»
пренебречь. Трение отсутствует. Массы грузов ти т г, т 8,
т, указаны на чертеже. — .
91. Тележка массы М=500 г скре’плена нитью с грузом
массы от=200 г. В начальный момент тележка имела скорость
t’j,=7 м/с и двигалась влево по горизонтальной плоскости
(рис. 35), Определить величину и направление скоро-»
сти тележки, место, где она будет находиться,„и путь, пройденный
ею, через й 5 с.
92. Для механической системы, изображенной на рис.
36, определить ускорения тел, массы которых отг, тг и от,.
Трение между соприкасающимися поверхностями отсутствует.
Массой блока А и нити пренебречь.
24 Динамика прямолинейного движения.
93. Между двумя неподвижными муфтами может без трещин
перемещаться вниз и вверх стержень, масса которого т.
Стержень нижним концом
касается гладкой поверхности’
клина массы М.
Клин лежит на гладком
горизонтальном столе
(рис. 37). Определить ускорения
Клина и стержня.
94. На стержень, длина
которого 21, надета бусинка
массы т. Бусинка
может перемещаться по
стержню без трения. В начальный
момент бусинка находилась на середине стержня.
Стержень поступательно передвигался в горизонтальной
плоскости е ускорением а в направлении, составляющем
угол а со стержнем (рис. 38). Определить ускорение бусинки
относительно стержня, силу реакции со ж ш »
стороны стержня на бусинку и время, через ч
которое бусинка покинет стержень.
95. Невесомая нить, перекинутая через
блок с неподвижной осью, пропущена
Рис. 37.
Рис. 39.
через щель (рис. 39); при движении нити на нее со стороны
щели действует постоянная сила трения F. На концах
нити подвешены грузы,
F М •* 00000 0 Л- т F ,
массы которых тх и т%.
Определить ускорение
грузов.
96. К концам пружины
прикреплены два
бруска, массы которых
равны М и т (М >т ). Под действием двух равных сил F,
приложенных к брускам, как показано на рис. 40, пружина
сжата. Бруски покоятся на столе. Что произойдет,
25 Динамика прямолинейного движения.
если силы F перестанут действовать? Коэффициент трения
брусков о стол равен &.
97. На задней стенке вагона на нити перекинутой через
гвоздь, висит картина. Как будет двигаться картина
относительно вагона, если нить оборвется, в случае, когда
1) скорость вагона возрастает? 2) скорость вагона убывает?
В обоих случаях абсолютная величина ускорения вагона
равна а. Коэффициент трения картины о стену вагона
равен к.
98. Два груза с массами mt и т2 связаны между собой
нитью, перекинутой через блок. Плоскости, на которых лежат
грузы, составляют с горизонталью углы а и р (рис.41).
Правый груз находится ниже левого на величину А.
Через время т после начала движения оба груза оказались
на одной высоте. Коэффициент трения между грузами и
плоскостями равен k. Определить отношение масс грузов.
99. Из точки О по желобам, лежащим в одной вертикальной
плоскости -и составляющим разнообразные углы с вертикалью,
одновременно начинают соскальзывать песчинки.
Найти геометрическое место точек, в которых окажутся песчинки
через время t, если коэффициент трения каждой песчинки
о желоб равен k.
100. Ледяная гора составляет с горизонтом угол а=30°;-
П0 ней пускают снизу вверх камень, который в течение
= 2 с проходит расстояние 1= 16м, после чего соскальзывает
вниз. Какой промежуток времени tt длится соскальзывание
камня вниз? Каков коэффициент трения между горой и
камнем?
101. Тележка массы М движется без трения по горизонтальным
рельсам со скоростью о0. На передний край тележки
кладется тело массы т. Его начальная скорость равна
нулю. При какой длине тележки тело не соскользнет с
нее? Размерами тела по сравнению с длиной тележки I пренебречь.
Коэффициент трения между телом и тележкой
равен к.
26 Динамика прямолинейного движения.
102. Брусок .массы М лежит на горизонтальной плоскости.
На бруске лежит тело массы т (рис. 42). Коэффициент
трения между телом н бруском, а также между бруском и
плоскостью, равен к. Исследовать движение при различных
значениях силы Л
п
м
ШЫ!3
1
11
ы—— ; / ———S-J
Рис. 42.
103. Брусок массы М лежит на гладкой горизонтальной
плоскости, по которой он может двигаться без трения.
На бруске лежит тело массы т (рис. 42). Коэффициент
треняя между телом и бруском равен к. При каком значении
силы F, приложенной к бруску в горизонтальном
направлении, тело начнет скользить по бруску? Через
сколько времени тело упадет е бруска? Длина бруска. /.
104. Стол весом Р х= 150 Н может без трения перемещаться
по горизонтальному полу. На столе лежит груз весом
Р 2—100 Н. К грузу прикреплена веревка, перекинутая через
два блока, закрепленных на столе (рас. 43). Коэффициент
трения между грузом и столом А=0,6. С каким ускорением
будет двигаться стол, если к свободному концу веревки приложить
постоянную силу, равную 80 Н? Рассмотреть два
случая: 1) сила направлена -горизонтально; 2) сила направлена
вертикально вверх.
105. На стержень, длина которого 21, надета бусинка
массы т. Коэффициент трения между бусинкой и стержнем
равен к. В начальный момент бусинка находилась на середа
27 Динамика прямолинейного движения.
не стержня. Стержень поступательно передвигается в горизонтальной
плоскости с ускорением а в направлении,
составляющем угол а со стержнем (рис. 38). Определить ускорение
бусинки относительно стержня, силу реакции со
стороны стержня на бусинку и время, через которое бусинка
покинет стержень. Силу тяжести не учитывать.
106. Старинная пушка, не имеющая противооткатного
устройства, стоит на горизонтальной площадке. Пушка
стреляет под углом а к горизонту снарядом, масса которого
т, а начальная скорость у0. Какую скорость будет иметь
пушка непосредственно после выстрела, если массй пушки
М, а ускорение снаряда в канале ствола значительно боль*
ше ускорения свободного падения? Коэффициент трения
между пушкой и площадкой равен k< .
107. Ракета имеет запас топлива т—8 тонн. Масса
ракеты (включая топливо) Л1= 15 тонн. Топливо сгорает
за 40 с. Расход топлива и сила тяги /*’=200 000 Н постоянны.
1 )-Ракета установлена горизонтально на тележке. Определить
ускорение, которое имеет ракета в момент запуска.
Найти зависимость ускорения от времени движения ракеты
р изобразить эту зависимость графически. По графику
оценить величину скорости, которую приобретает ракета
через 20 с после начала движения. Трение не учитывать.
2) Ракета запускается вертикально вверх. Измерения показали,
что через 20 с ускорение ракеты-было равно 0,8 g.
Рассчитать силу сопротивления воздуха, которая действовала
на ракету в этот момент. Ускорение g считать постоянным.
3) Для измерения ускорения ракеты на ней помещен
прибор, представляющий собой пружину, закрепленную
в вертикальной трубке. В покое пружина растянута прикрепленным
на ее конце грузом на ц— 1 см. Определить зависимость
растяжения пружины от ускорения ракеты. Начертить-
шкалу прибора.
108. Два кубика сложены вплотную и лежат на абсолютно
гладкой горизонтальной поверхности. Ребро каждого
кубика равно /, а масса равна М. В кубик попадает
пуля массы /л, летящая вдоль линии центров кубиков-.
Считая горизонтальную силу сопротивления, возникающую
при движении пули, постоянной и равной F, определить,
в каких пределах должна находиться начальная скорость
пули, чтобы последняя прошла через первый кубик и застряла
во втором
28 Динамика прямолинейного движения.
§ 4. Динамика прямолинейного движения. Ответы.
73. T = Fx/l.
74. Т — F xy/lh — действует в горизонтальном направлении
вправо. N = M ^ g — действует вертикально вверх.
75. Масса левой части стержня а правой
где М — масса всего стержня. Под действием приложенных к ним
сил каждая часть стержня движется с одним и тем же ускорением и.
Поэтому
/Л — F = 111^,
F — Fs = m2a. » ■
Отсюда растягивающая сила
F_ Fim2 + Fzm1 _ р L — l р I
Щ-\~т2 1 L ■ 2 L ‘
76. К бруску приложены две силы mg и N. Источником силы N
является деформированный пол лифта. Из уравнения движения бруска
ma = mg— N следует, что N = m(g — a). По третьему закону Нью- •
тона брусок (вследствие того, что он деформирован) действует на пол.
лифта с силой, равной N. Если a = g, то N = 0, т. е. брусок пере- —
стает действовать на пол (в бруске исчезли деформации). При ускоренном
движении вверх N = т (g + a ).
77. Чтобы доска не съезжала, составляющая силы, приложенной
к доске со стороны мальчика, должна быть направлена вдоль доски
вверх. Следовательно, на мальчика со стороны доски действует равная
и противоположная сила, направленная вдоль доски вниз. Выбрав
положительное направление координатной оси вдоль наклонной
плоскости вверх, запишем уравнения, движения мальчика:
— Mg sin а —F = Ма,
S = vat -g-, — ~ = v <s-{- at.
Доска находится в равновесии, поэтому F^—mg sin а = 0. Решив данную
систему, находим
‘ о ЗЛ^0
8 (М -\-т) g sin а ‘
78. Большее ускорение (о > g) у частиц бруска в верхнем сечении.
Частицы бруска в нижнем сечении в начальный момент времени
имеют ускорение a = g.
188 Кинематика криволинейного движения. Ответы.
79. В верхнем сечении в начальный момент времени частицы
бруска имеют ускорение a = g , в нижнем сечении—ускорение а > g.
80. Показания весов уменьшаются.
81. При движении крыльев воздух сжимается под крыльями и
разрежается над крыльями. Вследствие деформации воздуха возникает
подъемная сила N. Из уравнения движения ma = N —mg следует,
что N = ma-\-mg. По третьему закону Ньютона крылья мухи
действуют на воздух с силой N, направленной вниз. Вследствие
этого чашка весов, на которой находится бутылка с мухой; будет
опускаться.
82. На рис. 308 изображены силы, действующие на грузы. Уравнения
движения для грузов запишутся следующим образом:
тха — Т—т^,
m^a — m^g— Т,
где Т — натяжение нитй, а—ускорение. (Ускорения грузов одинаковы,
так как нить считается нерастяжимой. Невесомость нити и
блока определяет постоянство Т.) Отсюда а = [(m2 — m{)j(mx -f- т 2)] g=
=327 см/с2, Т — тг ( a + g ) = 1,3 Н. Время движения t = У~2Н/а я 1с.
У//////У/У////УУУЛ
Г г
Г м
4— ‘
F
F
ф :
Рис. 308.
Р
Рис. 309.
83. Если масса блоков и нити пренебрежимо мала (рис. 309),
то 2F —Т = 0, Г — Р = та. Отсюда F = (l -j-a/g) Р/2. При a = 0 F ~ P/i.
84. Уравнения движения для тел с массами тх, т2, т3 имеют
вид
mxa = mxg — Tx,
тф~т.’&—Т2,
mgc — ttisg — 7’g,
где а, Ь, с—ускорения относительно неподвижного блока А. Уско-
рение считается положительным,* если оно направлено вниз. Если
масса нити ничтожно мала по сравнению с массами тх, тг, т3^то
натяжение постоянно вдоль всей нити. Отсюда следует, что Т3—Т3,
и сила, с которой нить, перекинутая через блок А, действует на
блок В, равна Т х (рис. 310).
189 Кинематика криволинейного движения. Ответы.
Рассмотрим ту часть нити, которая находится в данный момент
времени на -блоке В. ‘На эту часть^ввртижалит свисающий;левый
конец нити действует с ‘силой Т2, а правый — с силой Т3 (Т2 = Т3).
Так как масса любой части нити ничтожно мала, то сумма всех действующих
на нее сил должна стремиться к нулю. Следовательно,
блок ‘В действует на лежащую на нем чаеть нити с силой F = Т2-\- Т 3,
направленной вверх. По третьему закону Ньютона деформированная
нить в свою очередь действует на блок с силой
Т2 ••’••• Тз. Так как масса блока В ничтожно
мала, то Т х- Т 2-\-Т3.
По прошествии некоторого времени (весьма
малого) после начала движения тел деформация
нитей прекращается, и длины после этого
не изменяются с течением времени. Это означает,
что ускорение блока В будет равно
( — а), а ускорения грузов тг и т3 относительно
блока В равны я Противоположны по направлению.
Обозначив через d ускорение тела
т2 относительно блока В, получим
& = ( — o) + rf,
с = (— а ) + (— d),
откуда Ь-\-с=—2а. Таким образом, окончательно
имеем следующую систему уравнений:
mia = m1g—Т,
mib==jntg —Tj2,
m3c = m3g — Т/2,
b J с- ••—2а.
Решая эту систему уравнений, уолучим (при условии m1~ m 2-\-m3)
а _ <т2-т 3У1 _ t
{ml~b-Jti3 -f- 6m2/ns) ’ ш? + 4т2т3
т\—4т3
_ . j ’т{ 4 т2т3
Т_ Smxm2m3
m\ -\-4m2m3
В ■ общем. случае
&т1т3т3
» 4т2т3 + тг (т2 -f т3)’
85. Показание динамометра вначале равно F = 30H. Если показания
динамометра не меняются, то на груз 20 Н действует направленная
вверх сила натяжения нити, ;равная ЗОН. Следовательно,
этот груз движется вверх с ускорением a = g / 2. С тем же ускорением
.движется -вниз другой груз. Дополнительный груз на второй чашке
находится- из уравнения .
г.
откуда Рх
190 Кинематика криволинейного движения. Ответы.
Отсюда Г = 0 и a1 = ai = g. Оба груза* свободно падают с ускорением
g Блоки В и С вращаются Против часовой стрелки, блок Л —
по часовой стрелке.
89. Пусть в некоторый момент i-й груз находится на расстоянии
xi от потолка. Тогда из нерастяжимости всех нитей следует, что
сумма всех таких расстояний остается во время движения постоян-
8
ной: 2 * 1 = £. За время At произойдет изменение каждого из’ этих
»=1
расстояний, поэтому через время Д^
8 » a{(At)*i
£ ^xt + Vi A t+ a’ ^ j =&.
i=i
Вычитая одно уравнение из другого, получим после сокращения
на At:
1=1 1=1 1=1
Поскольку это равенство должно быть справедливым при любом At,
г ®
ускорения грузов связаны соотношением 2 % = 0 . Так как массы
191 Кинематика криволинейного движения. Ответы.
блоков и трение в их осях пренебрежимо малы, то натяжение одной
и той же нити, перекинутой через любой блок, по обе стороны блока
одинаково и равно половине натяжения той нити, на которой этот
блок висит. Отсюда следует, что натяжения всех нитей, на которых
висят грузы, равны’между собой. Обозначив это натяжение через Г,
запишем уравнение движения /-го груза в виде*
90. Обозначим натяжение нити, на которой висят грузы т , и т 2,
через Т. Тогда натяжение нити, на которой висит груз т 3, равно 27,
а натяжение нити, на которой висит груз т 4, равно 4Т. Уравнения
движения для грузов запишутся в виде
Из-за — нерастяжимости нитей ускорения грузов связаны соотношением
(Это соотношение можно получить тем же способом, как в решении
задачи 89.) Решив полученную систему уравнений при заданных
значениях тъ т.ъ т3, /л4, найдем a4= g /33 и 0,3 м/с2.
91. Для данного случая уравнения динамики запишутся в виде
будет находиться на том же месте (х = 0) и будет иметь скорость
vt — 7 м/с, направленную вправо. Тележка пройдет
195 Кинематика криволинейного движения. Ответы.
92. На рис. 312 изображены стрелками все силы, действующие
на тела тъ т2, т3. Обозначим через а ускорение тел тг и пц,
а через с и b—горизонтальное и вертикальное ускорения тела т3.
Запишем проекции уравнений движения на горизонтальное и вертикальное
направления:
m1a=m 1g —T, m2a=T-f-W sin а,
m3b=m 3g—N cos ос, /п3с = N sin а.
Из геометрических соображений следует соотношение b/(a-\-c) = tg a .
Решая эти уравнения, находим а, Ь, с:
а = M——i +—/к32- -s-i-n- -a— -c-o—s- а а
-f- т2 tu3 sin ct
^ sin а cos a + (m i+ m 2 + m3) sin2a
* m1 + m2 + m3 sin2 a
m2) sin a cos a —ml sin2a
C== nij^+mj+mg sin2 a ^ ‘
Ранение справедливо при tg a — 1 < Щ/Щ (см. задачу 35).
93. На рис. 313 изображены все силы, действующие на стержень
н клин. Обозначим через а ускорение стержня относительно неподвижного
стола, а через Ь—ускорение клина. Запишем проекции
уравнений движения стержня и клина на горизонтальное и вертикальное
направления:
ma=mg—N cos а , 0 = Л ^—N3-\-N sin a,
Mb = Ns in a , 0*=N3 — N c o sa—Mg.
Из геометрических соображений следует уравнение кинематической
7 Б. Б. Буховцев в др. 193
196 Кинематика криволинейного движения. Ответы.
евязй !между уеввревшм*?сгераа» eaoewBaopfrfetg^»; Решая; урав-
нения, получаем ,
тЦ*Ъг< b=L m i g *
M + tn tg2oc®’ Af + mtg2a s
94. Единственной силой, действующей на бусинку, является сила
реакции стержня N, которая направлена перпендикулярно стержню.
Абсолютное ускорение wa бусинки; (ускорение относительно неподвижного
наблюдателя) будет направлено в сторону действия силы
реакции N. Относительное ускорение w0. направлено вдоль стержня
(рис, 314); wa = a -fw 0. Из треугольника ускорений следует:
и)0= а cos a, wa ~ а sin сс. На основании второго закона Ньютона
сила реакции равна N = та sin а . Время движения бусинки по
стержню т определяется из уравнении; 1 = (а cos а)т2/2. Отсюда
т = УЩ а cos а).
Рис. 315.
95. Рассмотрим элемент нити, находящийся в щели. Пусть нить
движется; вниз. Тогда* на элейент нитй ; дейвтвукян силы н|тяжения
нитичс обеих; сторон; № сила* трети :(рие;.: 315^,* Так как массой рассматриваемого;
кусочка — ниш ‘ мы;; пренебрегаем;’ та 7^—F’—T’i—Ш
Уравнения’ динамики запишутся; следующим‘ образом;
triig—T1 = m1a, rrtig—Т г——пца.
Отсюда
д—(Щ—тг)В—F
/Пх+Ша
96. 1) Если F ^.kmg, то бруски‘не будут двигаться.
2) Есяя: kM§ c ^ f’>>kmgii. то:, б,удег; двигаться меньший брусок.
3) Если F > kMg, та бруски будут двигаться в разные стороны.
(Предполагается; что пока действовали силы F, трение отсутствовало.)
97. 1) Если скорость вагона возрастает, картина будет скользить
вдоль задней’стеяки’ вагона вниз с ускорением;#-—й& (Если йв > # ,
то картина будет находиться в покое.)
2) Если скорость вагона убывает, картина будет двигаться вниз
с ускорением g и вперед с ускорением а.
98. По второму закону Ньютона
(тх+щ) а = fftjf Bin ■а.— sin Р—fcWjg cos ot— й т ^ соя р.;
197 Кинематика криволинейного движения. Ответы.
удовлетворяющего
следующим уравнениям:
SМ п я= Н—Ssin Р, S==aiг2/2.
Исключая S и а из системы трех уравнений*, получим
т, g r2 (sintx+,sinP) (feeoaft -М> П’Р)+2А
/л8 gx2 (sin а + sin (3) (sin а —ft cos ое)—2А’
99. Рассмотрим желоб, составляющий произвольный угол <р с вертикалью
(рис. 316). Если ft < c tg f, то дуть, пройденный песчинкой,
S = a l2/2, где a= g (co s <р —………
— ft sin-ф). Координаты песчинки:
х = 5з1Пф, у = 5 с о зф . 0т-
сюда
x2+ y 2= S 2 =
или
{х*+у*Г = (5т?{у-*кх)*.
Учтем, что ft < у/х, и обозначим
A ==g/2/4. Тогда
х2+ у 2 = 2Л (р— ftx).
Последнее уравнение можно записать
в виде
(* +АЛ )2+ (у—Л)2 = Л«( 1-fft2).
Это—уравнение окружности радиуса R = A j / ”l + ft2= ^ 1+ft2
с центром, лежащим-ниже тонки О на Л* и левее .вертикали
на kA = kgt2/4. По другую сторону вертикали геометрическое место
искомых точек составляет аналогичную дугу.
100. Уравнения движения дают для ускорения камня следующие
выражения:
co&a) шри движении вверх,
—ft»cosia) -при-движении вниз.
Кинематические уравнения запишутся следующим образом)
/ = o0/ i— fli?i/2,. / = аа/1/2, о0—ах/1 = 0.
Из этих пяти уравнений находим
gif соз а ‘ о
1
g t i s in a—1
-*—= 4 ,2 с.
101. Тележка первоначально движется равнозамедленно. Скорость
тележки равна v= v 0—(f/M) t, где / —сила трения, равная kmg.
Тело движется равноускоренно. Скорость тела и = ( //т )1 . Если
198 Кинематика криволинейного движения. Ответы.
Эго произойдет в момент времени x= v 0Hf/m-^-f/M). После этого
и тело, и тележка начнут двигаться с постоянной скоростью, равной
Тележка к этому моменту времени пройдет путь S =
= о0т —(//2Л1)т2, а тело—путь s = (//2m) т2. Путь, пройденный телом
относительно тележки, равен S —s. Этот путь должен быть меньше /.
Таким образом, тело не покинет тележку при условии S—s < / , т. е.
102. Если k (m-\-M)g, движения нет. ПустьF > k(m-j-M)g.
Исследуем случай отсутствия скольжения тела по бруску. Уравнения
движения при этом будут иметь вид
Если же F > 2k (m +M )g , то тело будет скользить по бруску. В этом
случае уравнения движения имеют вид
где / —сила трения, а и 6 —ускорения. Предположим, что проскальзывания
нет, тогда а — Ь. Из уравнений движения можно определить
ускорение и силу трения. Сила трения f = mF/(M-{~т). Чтобы не
было проскальзывания, сила трения должна удовлетворять неравенству
f< km g , т. е. F/(M-\-m)<kg. Если F > k(M-\-m)g, то возникает
скольжение. Уравнения (1) и (2) в этом случае примут вид
Из этих уравнений находим а и b: a = kg, b = (F — kmg)/M. Очевидно,
что b > а. Ускорение тела относительно бруска будет направлено
в сторону, противоположную движению, и по величине
равно (F-~kmg)jM — kg. Время движения тела по бруску т =
199 Кинематика криволинейного движения. Ответы.
рис. 317. Уравнения движения по горизонтали имеют следующий вид:
для стола с блоками
F — F + F тр
Pi а,!
для груза
Р — Р* а
Предположим, что сила F настолько мала, что груз не скользит по
столу. Тогда а1 = а2 и Flp = FP1/(P1+ P 2). Увеличивая постепенно
силу F, мы тем самым будем постепенно увеличивать и силу
трения Frр. Однако если стол и груз неподвижны друг относительно
друга, то сила трения между ними не может превысить значения
F.гР Шах = кР2. Поэтому скольжение груза, по столу начнется при
F > FiV ш а * = k (p i + Р*У= 100 Н.
В нашем случае F = 80H, следовательно, груз проскальзывать не
будет и
р g
ai = ai= — p — f p ^ S = — ^ ) 8 ^ ^ M м/с2.
2) Уравнения движения для стола с блоками и груза в этом
случае имеют вид
_ F + F Tp= A a i, «FF тр—- Рg* аа г-
Ускорения стола и груза направлены в противоположные стороны,
поэтому проскальзывание обязательно будет. Следовательно, FTp =
= kP2. Ускорение стола равно
2
ах- : F + kl>*g = — ^Т5gг * -1 ,3 1 М/С2 .
Стол будет двигаться влево.
200 Кинематика криволинейного движения. Ответы.
ОТГ. При движении бусинки* на нее действуют две силы: сила
трения* № 0 v силг реакции N’. Абсозгогное ускорение будет направлено
по результирующей силе F. Из рис. 318 следует:
N =та sin a, t%f=a cos,a—Ш1т=*а (cos a—ft sin a).
I ‘ a (cos a —ft sin a)
Если ft Ss ctg a, то бусинка не будет двигаться относительно стержня,
и в этом случае сила трения равна т а cos а.
106. По второму закону Ньютона изменение количества движения
системы пунша—снаряд за время выстрела т должно равняться
импульсу действующих на систему сил:
по горизонтали
mv0 cos a —Mv1 = FTpx,
где FTpT—импульс сил трения;
по вертикали
mv0 sin a = Nx—(Mg+ mg) x,
где Nx—импульс сил нормального давления (реакции горизонтальной
площадки), (Mg-\-mg)x—импульс сил тяжести. Учитывая, что
FTV=kN, получим
т и т ■ t. М-\-т P l = — ^ — P 0 C O S « — fe -^ g -P f fS inC C — f t — ^ g x ^
или, так как gx о0.
Vi « (cos a —ft siri a).
Данное решение пригодно для ft < ctg а. При ft* >• ctg a пушка останется
неподвижной:
107. 1) Ускорение в начальный момент a<, = F/M я 13,3 м/с2.
В Зависимости от времени ускорение меняется по закону a= F/(/H—fi().
201 Кинематика криволинейного движения. Ответы.
где -fiWSeO кг/с—маеса топлива, расходуемая ракетой в секунду.
Г рафик ускорения имеет вид, изображенный на рис. 319. Скорость
спустя 20 с численно равна площади, заштрихованной на чертеже,
v ж 300 м/с.
2) Второй закон Ньютона запишется так:
(М— pt)a = F — (М— {ii)g—f.
По условию /= 2 0 с, a—Q,8g. Отсюда сила сопротивления воздуха
f= F —(M-p/ )2— 125-10» Н.
3) У равнение Ньютона для груза .дает тха ~ к х—т ^ , где тх —-
масса груза на конце пружины, а—ускорение ракеты, А —коэффициент
упругости пружины, х — удлинение пружины. По условию
задачи m1g = fc/0. Следовательно, x —~ ( a + g). Шкала прибора
должна быть равномерной. Делению в один сантиметр соответствует
ускорение g. •
108. В системе отсчета, связанной со вторым кубиком, имеем
of— Ро— 2а{1, — of = 2д2/,
где -ах = — F (2М т)/2Мт — ускорение пули в первом кубике,
ог — ее скорость при выходе из него, о2= —F (М -ir m)/Mm — ускорение
пули во втором кубике, v2— ее скорость при выходе из
него. Положив vx = 0, найдем нижний предел скорости »0, а „положив
v2 = 0, получим верхний .предел. Следовательно,
202 Кинематика криволинейного движения. Ответы.