ЛАБОРАТОРИЯ «КВАНТА»

Опыты с маятниками.

Г.Л.Коткин

Страница переведена на новый сайт https://myeducation.su/ : страница

ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЖУРНАЛ Квант (1 1972)

Трудно найти физические приборы,
которые были бы так просты по уст-
ройству и надежны в употреблении,
как маятники. .Между тем, опыты
с ними могут привести к любопытным
результатам, которые чрезвычайно
важны не только в механике, но и
в радиотехнике и электротехнике.
Попробуйте самостоятельно про-
делать предлагаемые опыты и объ-
яснить те эффекты, ьоторые вы при
этом будете наблюдать. Хотя сами
опыты очень просты, однако, пол-
ностью разобраться в поведении маят-
ников непросто: для этого нужно
знать основные законы гармоничес-
ких колебаний и иметь опыт в три-
гонометрических преобразованиях.
Полностью разобраться в данной
статье смогут, по-видимому, лишь
только десятиклассники, однако и
школьники 8—9 классов могут про-
делать эти опыты и полностью объяс-
нить их хотя бы качественно.

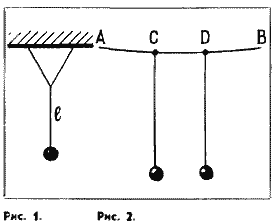
Маятник с раздвоенным подвесом

Сделайте маятник с раздвоенным
подвесом, показанный на рисунке 1.
Длина нити маятника / должна
быть намного больше длин нитей
верхней раздвоенной части под-
веса.
Толкните маятник под углом к
плоскости рисунка. Вы увидите, что
26
сначала маятник будет качаться в
направлении толчка, но вскоре его
движение перейдет во вращение во-
круг вертикальной оси. Затем маят-
ник вновь начнет колебаться в
плоскости, но уже не в той, в кото-
рой его толкнули. После этого снова
начнется вращение, но уже в другую
сторону. Постепенно оно сме-
нится движением в напраааении пер-
воначального толчка. Потом все опять
повторится сначала.
С чем связано такое поведение
маятника?

Связанные маятники

а) Два одинаковых маятника (на-
пример, гайки на нитке) подвесьте
на не очень туго натянутой нити
АВ (рис. 2). Отклоните один из ма-
ятников и отпустите.

26 ЛАБОРАТОРИЯ «КВАНТА» . 

Попробуйте менять массы гру-
зиков, изменять длины нитей маят-
ников, натяжение верхней нити.
б) Прикрепите два маятника к
жесткой раме. Затем свяжите нити
маятников ниткой на некоторой вы-
соте (рис. 3). Отклоните один из
маятников и отпустите. Посмотрите,
как при этом будут двигаться маят-
ники.

Двойной маятник

Устройство двойного маятника пс-
казано на рисунке 4. Верхний грузик
намного тяжелее нижнего, а длины
нитей одинаковы. Толкните нижний
грузик и наблюдайте за его дви-
жением.
Давайте теперь разберемся в по-
ведении этих маятников.
1. Начнем с маятника с раздво-
енным подвесом.
Довольно сложное поведение ма-
ятника, которое вы наблюда-
ли, можно объяснить тем, что его
движение складывается из двух ко-
лебательных движений (рлс. 5): па-
раллельного плоскости гу и перпен-
дикулярного ей. Эти колебания про-
исходят независимо друг от друга
(если отклонения маятника от вер-
тикали не слишком велики), а перио-
ды их соогв*тственно равны
7\ = 2л 1/Z и Г2 = 2л \ГЦ.
‘ g * S
Прежде всего научимся описывать
движение грузика с помощью ко-
ординат.
Пусть точка А движется по ок-
ружности радиуса а с угловой ско-
ростью с» против часовой стрел-
ки (рис. 6а) или по часовой стрел-
ке (рис. 66). Тогда проекция В точ
ки А на ось х совершает гармони-
ческие колебания*)с угловой часто-
той ш, равной —-. и амплитудой а.
Проекция С той же точки А на ось у
совершает подобные же колебания,
но достигает наибольшего отклонения
от точки О на четверть периода
позже — через время, за которое ра-
диус ОА делает — оборота вокруг
точки 0. В этом нетрудно убедиться,
проследив за движениями точек С
и В при вращении радиуса ОА. В тот
момент, когда проекция точки А на
ось х максимально отклонена от точ-
ки О, ее проекция на ось у как раз
¦ *)См.. например, статью Я. Л. Смородин-
ского «Похожие движения», «Квант» .\s 9,1971.

27 ЛАБОРАТОРИЯ «КВАНТА» . 

проходит через точку О и наоборот.
То, что мы говорили, можно выра-
зить и при помощи формул.
Из рисунка 6 а видно, что
х = ОВ =¦ a cos (р — a cos со/,
у = ОС — a si п ф ^ a sin to/ —
¦•^оcos (со/— -^ Wacoscof/—^-J
(О
Формулы A) справедливы при л кэ-
бом угле, а не только при остром.
(Это следует из определений коси-
нуса и синуса).
Если движение точки А проис-
ходит по часовой стрелке (рис. 6 6),
то, проследив за движениями то-
чек С и В, можно заметить, что коле-
бание точки С опережает колебание
точки В на четверть периода. Впро-
чем, можно сказать, что колебание
точки С на три четверти периода
отстает от колебания точки В. Так
как в этом случае угол со/ считается
отрицательным, то
х = a cos (— со/) = acos to/,
у = asin ( — to/) — — a sin со/—
{ — a cosf со/ -г ~y ] — a cos( со/ —~-) =
B)
\Ь формул (I) и B) видно, что ко-
ординаты х и у периодически меняют-
ся с течением времени Л Это озна-
чает, что точки В и С совершают
колебательные движения.
Пусть теперь точка А вместо дви-
жекня по окружности совершает гар-
монические колебания вдоль прямой
EOD (рис. 7) с частотой со и амплиту-
дой Ь — 0D = ОЕ. В этом случае обе
проекции В и С колеблются и одно-
временно достигают наибольших от-
клонений в положительных и отрица-
2л
л
•) Тлк как « — — , то ^77
Г/ О COS 0) [ ‘-
18
— -г- »
с
/
k° \
0 В х 0
с
У
В
4х
Е’
Рис. 7.
Рис. 8.
тельных направлениях осей х и у
и одновременно проходят через точ-
ку О. Точки В » С, как говорят,
колеблются «в фазе». Положим для
простоты, что *4 D0x = -^- . При
этом амплитуды колебаний точек В
и С одинаковы и равны
?>cos-r-=
4
л
4
Поскольку OB — b cos «/, получаем
Если же точка А колеблется вдоль
прямой E’D’ (рис. 8), то в момент
наибольшего отклонения точки В в
положительном направлении оси а’
отклонение точки С имеет наиболь-
шую величину в отрицательном на-
правлении оси у. В этом случае го-
ворят, что колебания точек В и С
совершаются «в противофазе». Можно
считать также, что колебание точки С
отстает от колебания точки В на пол-
периода (или опережает на полпери-
ода — в данном случае это все равно).
Тогда
х= —?=: cos со/,
1/2
У «= — у= cos со/ — y-cos (to/ — л) =
Вернемся теперь к нашему маят-
нику. Если его грузик отклонить в

28 ЛАБОРАТОРИЯ «КВАНТА» .

направлении 0D (рис. 7) на рассто-
яние а и затем отпустить, то коор-
динаты грузика будут изменяться со-
гласно формулам:
E)
где
2л -ш/~Т
2л
Напомним, что / и L очень мало
отличаются друг от друга, то есть
частоты со, и со4 почти одинаковы.
Поэтому вначале колебания по
осям х и у происходят почти в фазе.
Так как u^coj, то с течением
времени колебание по оси у отстает
от колебания по оси х все больше
и больше. Но, как мы видели, при
движении точки по окружности про-
тив часовой стрелки колебания ее
проекций на оси х и у отстают друг
от друга на четверть периода. Отсюда
следует, что когда отставание ко-
лебаний грузика по осям х и у достиг-
нет четверти периода, он будет дви-
гаться как раз по окружности против
часовой стрелки. При отставании ко-
лебаний грузика по осям х и у на
полпериода он будет двигаться вдоль
прямой E’D’. Затем отставание коле-
бания вдоль оси у достигает -^ перио-
да — грузик движется по окружности
по часовой стрелке. Наконец, при от-
ставании на целый период грузик
опять колеблется вдоль прямой ED.
Это вы и наблюдали.
Эти рассуждения удобно «пересказать»
с помощью формул. Систему E) можно пред-
ставить в виде
F)
у—a cos (a,/—ф).
где <р — (о^ — (L>t)t. За два-три периода
Ф почти не изменяется, но за много
периодов неуклонно нарастает. При
Ф = О, -iL , л, — формулы F) совпадают
последовательно с формулами C), A), D). B).
Рис. 9.
При ф — 2л грузик возвращается к
движению по прямой ED.
Изложенную теорию можно проверить
экспериментально. Ведь мы можем рассчитать,
через какое время движение грузика пройдет
весь цикл изменений. Если »го время Тс, то
. _ „ 2л
<Ро=(ю1—ю,) Т„=2я. откуда =- =ш,— щ,
‘ D
НЛИ
G)
Теперь нужно измерить периоды колеба-
ний Ti и Tt маятника, заставив его колебать-
ся одни раз в плоскости уг, другой раз —
в плоскости хг. Время То измеряется неза-
висимо. Измерив Тг, Тг к То, проверьте пра-
вильность формулы G). Для намерения 7″,
и Тг лучше определить время, скажем, в
10— J5 колебаний. Тут же обнаруживается,
какие причины ведут к отклонению от расче-
тов. По-видимому, прежде всего сказывается
затухание колебании, вызванное сопротивле-
нием воздуха. Что же. грузики не должны
быть слишком легкими.
В действительности движение происходит
не по прямой или окружности, а по сложной
траектории. Эта траектория (рис. 9) более нли
менее равномерно «заполняет» весь квадрат.
Если начальное отклонение составляет
с плоскостью симметрии угол, отличный от
я
~4~, то характерными «мгновенными» траек-
ториями грузика оказываются диагонали
прямоугольника и вписанные в него эллипсы.
Тот факт, что движение маятника скла-
дывается из независимых колебаний, выража-
ют, говоря, что для его колебаний справедлив
принцип суперпозиции *).
2. Перейдем к объяснению движе-
ния связанных маятников (рис. 2 и 3).
Если отклонить, а затем отпустить
один из них, мы увидим, что посте-
пенно придет в движение другой.
*) Читатели «Кванта» уже встречались
с принципом суперпозиции при объяснении
вида волн иа поверхности воды («Квант» № 1.
1971, стр. 32).

29 ЛАБОРАТОРИЯ «КВАНТА» .

Это объясняется тем, что при от-
клонении первого маятника связы-
вающая их нить деформируется и
сила упругости воздействует на дру-
гой маятник, сообщая ему ускорение.
Первый маятник будет колебаться
со все меньшей амплитудой и, на-
конец, остановится. В это время ам-
плитуда колебаний второго маятника
будет наибольшей. Потом раскачает-
ся первый маятник, а второй оста-
новится и так далее.
Сложное колебательное движение
системы, состоящей из двух маятни-
ков, можно представить как резуль-
тат сложения (суперпозиции) двух
колебаний с частотами о, и <о2. Одна
из частот равна частоте, с которой
будут колебаться оба маятника, если
их одновременно отклонить в одну
сторону, а затем отпустить (рис. 10).
Обозначим эту частоту через со^ Дру-
гая частота ш2. Это частота, с кото-
рой будут колебаться оба маятника,
если их вначале одновременно от-
клонить в противоположные стороны,
а затем отпустить (рис. 11).
Отметим, что угловая частота ю2
больше угловой частоты ы^ Эти два
колебания называются нормальными
колебаниями двух связанных маят-
ников.
Напншем уравнения нормальных
колебании. Первое
ixj *=
\х\ — —a
^ a cos uy.
Сложим смещения лг/ с *,» и х2′
с х2″. Получим:
Воспользовавшись формулой сло-
жения косинусов, получим:
г. / ь>,—о>, Л / О),-{-to. Л
— 2аcos/ ‘ 2 f Mcosf i J * t\.
х. =
= 2flSinf ‘ 2 * /Jsm I ‘g t\.
Полученное выражение для х^ мы
можем написать в следующем виде:
Вследствие того, что to! мало отличает-
ся от to4, выражение cos —’—^——t\
близко к 1 (если ш, равна ш2, то
это выражение равно 1). С1едователь-
но, оно мало влияет на значение хх.
Поэтому сомножитель 2а cos (Ц1Т -11
в выражении для xt можно рассмат-
ривать как медленно изменяющуюся
амплитуду (красный пунктир
на рис. 12, о). Аналогично обстоит
Рис. 12.

30 ЛАБОРАТОРИЯ «КВАНТА» .

Это объясняется тем, что при от-
клонении первого маятника связы-
вающая их нить деформируется и
сила упругости воздействует на дру-
гой маятник, сообщая ему ускорение.
Первый маятник будет колебаться
со все меньшей амплитудой и, на-
конец, остановится. В это время ам-
плитуда колебаний второго маятника
будет наибольшей. Потом раскачает-
ся первый маятник, а второй оста-
новится и так далее.
Сложное колебательное движение
системы, состоящей из двух маятни-
ков, можно представить как резуль-
тат сложения (суперпозиции) двух
колебаний с частотами о, и <о2. Одна
из частот равна частоте, с которой
будут колебаться оба маятника, если
их одновременно отклонить в одну
сторону, а затем отпустить (рис. 10).
Обозначим эту частоту через со^ Дру-
гая частота ш2. Это частота, с кото-
рой будут колебаться оба маятника,
если их вначале одновременно от-
клонить в противоположные стороны,
а затем отпустить (рис. 11).
Отметим, что угловая частота ю2
больше угловой частоты ы^ Эти два
колебания называются нормальными
колебаниями двух связанных маят-
ников.
Напншем уравнения нормальных
колебании. Первое
ixj *=
\х\ — —a
^ a cos uy.
Сложим смещения лг/ с *,» и х2′
с х2″. Получим:
Воспользовавшись формулой сло-
жения косинусов, получим:
г. / ь>,—о>, Л / О),-{-to. Л
— 2аcos/ ‘ 2 f Mcosf i J * t\.
х. =
= 2flSinf ‘ 2 * /Jsm I ‘g t\.
Полученное выражение для х^ мы
можем написать в следующем виде:
Вследствие того, что to! мало отличает-
ся от to4, выражение cos —’—^——t\
близко к 1 (если ш, равна ш2, то
это выражение равно 1). С1едователь-
но, оно мало влияет на значение хх.
Поэтому сомножитель 2а cos (Ц1Т -11
в выражении для xt можно рассмат-
ривать как медленно изменяющуюся
амплитуду (красный пунктир
на рис. 12, о). Аналогично обстоит
Рис. 12.

Кроссворд МФТИ

Существует много видов студенческо-
го фольклора: песни, анекдоты, сказки.
У студентов Московского физико-техничес-
кого института, кроме всех перечиспенных
существует еще один — кроссворды.
Для того чтобы разгадать такой кросс-
ворд, необходимы в первую очередь чув-
> ство юмора и фантазия. Энциклопедии и
справочники тут не помогут. Среди пре-
подавателей МФТИ отличным достижением
считается отгадывание поповины слов крос-
сворда, среди студентов показатели не-
сколько выше. Если приведенный ниже
кроссворд ие будет вам поддаваться, то
посмотрите на страницу 38, где расшифро-
вываются слова по горизонтали, и выпиши-
те их, после этого попытайтесь самостоя-
тельно отгадать слове по вертикали. Отве-
ты на них даны на странице 65.

По горизонтали: 1. Вычислитель-
ный центр научно-исследовательского ин-
ститута по организации отдыха трудящихся
производственно-учебного строительного
комбинате. 6. Черт в ночи. 7. Далеко.
8. Природное соединение. 11. Персонаж
русский народных сказок, появляющийся
преимущественно из-за гор. 13. Музыкаль-
ный инструмент без звука. 14. Среднеазиат-
ский сатирик, философ, композитор, поэт и
певец. 17. Терпеливый казак. 20. Сын восто-
ка. 21. Приспособление для остановки по-
езда путем нажатия кнопки. 22. Фокус со
светом.
По вертикали: 1. Нехороший чело-
век и к тому же пьющий. 2. Тонкость.
3. Произведение П. И. Чайковского. 4. Род
угля. 5. Очковый змей. 9. Одинокий оби-
татель дикого севера. 10. Силой протяжения
к Земле. 12. Очень большая шкала. 15. Че-
ловек с лопатой. 16. Легендарное сокраще-
ние штатов. 18. Не голод. 19. Несколько
одинаковых букв.

31 ЛАБОРАТОРИЯ «КВАНТА» .

 Кардиоида

Фнгура, изображенная на первой стра-
нице обложки, представляет собой одну из
замечательных кривых — кардиоиду. Слово
«кардиоида» означает в переводе с греческого
«сердцевидная».
Впервые изучал свойства этой кривой
в 1674 голу французский академик Оле
Ремер.
У кардиоиды много «родственников»-
Это прежде всего различные циклоиды, эпи-
циклоиды и гипоциклоиды.
Если окружность катится по прямой, то
ючка, закрепленная иа этой окружности,
оставляет на плоскости ¦ след — кривую, ко-
торая называется циклоидой (рис. 1).
Если подвижная окружность катится по
внутренней части неподвижной окружности,
то точка, закрепленная на первой из них,
описывает на плоскости кривую, которая
называется гипоциклоидой (рис- 2).
Если же подвижная окружность ка-
тится по наружной части неподвижной
охружности, то кривая, которую описывает
точка, лежащая иа подвижной окружности,
называется эпициклоидой (рис. 3).
Кардиоида — это эпициклоида, у кото-
рой подвижная и неподвижная окружно-
сти одного и того же радиуса ¦ (см.
рис. 4).
Об особенностях всех этих циклоид,
в том числе кардиоиды, вы можете про-
честь, в книге Г. Н. Бермана •Цикло-
ида», (Гостехнздат, 1954).
На рисунке 5 показано одно из возмож-
ных построений кардиоиды. Неподвижная
окружность разбивается точками на участки.
Из каждой такой точки, как из центра,
проводятся окружности, проходящие тгкже
через одну фиксированную точку на этой же
окружности. Попробуйте доказать, что при
таком построении вы» действительно получа-
ете кардиоиду (описанную около всех этих
окружностей).
В заключение — забавная интерпрета-
ция кардиоиды- Рассмотрим не скользкую,
круглую в поперечном сечении неподвижную
талию. Около нее вращается обруч хула хуп
вдвое большего радиуса. Тогда каждая
точка обруча описывает около талии кар-
диоиду.
М J1. С Полянский

32 ЛАБОРАТОРИЯ «КВАНТА» .

 

ЛАБОРАТОРИЯ «КВАНТА»