Глава I . МЕХАНИКА.
Страницы переведены на новый сайт:
СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ
https://myeducation.su/sbornik-zadach-po-elementarnoj-fizike/
1. Кинематика равномерного прямолинейного движения.
1. Идущая вверх по реке моторная лодка встретила
_ сплавляемые по течению реки плоты. Через час после встречи
лодочный мотор заглох. Ремонт мотора продолжался
30 мин. В течение этого времени лодка свободно плыла вниз
по течению. После ремонта лодка поплыла вниз по течению
с прежней относительно воды скоростью и нагнала плоты
на расстоянии S—7,5 км от места их первой встречи. Определить
скорость течения реки* считая ее постоянной.
2. Из Москвы в Пушкино с интервалом t= 10 мин вышли
два электропоезда со скоростями о=30 км/ч. С какой
скоростью и двигался поезд, идущий в Москву, если он
повстречал эти электропоезда через т—4 мин один после
другого?!
3. Завод, на котором работает инженер, находится за
городом. Каждый раз к приходу поезда на станцию’приезжает
заводская машина, которая-доставляет инженера, на
место работы. Однажды инженер приехал на станцию на
час раньше обычного и, не дожидаясь машины, пошел на
завод пешком. По дороге он встретил автомашину и приехал
на завод на 10 минут раньше обычного. Сколько временя
шел инженер до встречи с заводской автомашиной?
(Решить задачу графически.)
4. Трое туристов, обладающих одним велосипедом,
должны прибыть на базу в кратчайший срок (время оценивается
по последнему прибывшему). Велосипед может взять
лишь двоих, поэтому третьему туристу приходится сначала
идти пешком. Велосипедист довозит второго туриста до некоторой
точки дороги, откуда тот продолжает движение пешком,
и возвращается за третьим. Найти среднюю скорость
туристе®, если скорость пешехода Oi=4 км/ч, а велосипедиста
оа=20 км/ч.
7 МЕХАНИКА.
5. Почтовая связь между речными пристанями М и К
осуществляется двумя катерами. В условленное время ка-
теры отплывают от своих пристаней, встречаются, обмениваются
почтой и возвращаются обратно. Если катеры отплывают
от своих пристаней одновременно, то катер, выходящий
из М , тратит на путь в оба конца 3 часа, а катер
из К — 1,5 часа. Скорости обоих катеров относительно воды
одинаковы. Определить графически, на сколько позже
должен отплыть катер из М после отплытия катера из К,
чтобы оба катера находились в пути одно и то же время.
6. Используя условия предыдущей задачи, определить
скорость катеров относительно воды, скорость течения
реки и место встречи катеров в случае, если они отплывают
от своих пристаней одновременно. Расстояние между при —
станями равно 30 км.
7. От пристани С к пристани Т по реке плывет со
скоростью 1^=3 км/ч относительно воды весел|рая лоДка.
От пристани Т к пристани С одновременно с лодкой отходит
катер, скорость которого относительно воды v2~ ГО км/ч.
За время движения лодки между пристанями катер успевает
пройти это расстояние четыре раза и прибывает к
Т одновременно с лодкой. Определить направление течения.
8. Человек высотой А проходит в стороне от фонаря,
висящего на высоте Я над землей. Найти величину и . направление
скорости перемещения по земле тени от головы
человека, если скорость человека равна v.
9. Две свечи, высоты которых в начальный момент были
одинаковы и равны А, находятся на расстоянии а друг
от цруга. Расстояние между д
каждой свечой и ближайшей
к ней стеной также равно а (рис. 1). С какой скоростью движутся
тени от свечей по стенам, если одна свеча сгорает за
время tu а другая— за /*?
8 МЕХАНИКА.
10. Человек ‘ находится на берегу озера в точке А.
Ему необходимо в кратчайшее время попасть в точку В, находящуюся
на озере (рис. 2). Расстояние от точки В до берега
BC=*d, а расстояние ЛС =5. Скорость движения человека
в воде Oi, а по берегу o2(os>i»i). Каким путем должен
двигаться человек: плыть ли из точки А по прямой АВ или
пробежать по берегу некоторое расстояние и после этого
плыть по направлению к точке 5?
11. По шоссе со Скоростью et==16 м/с движется автобус,
а человек находится на расстоянии о—60 м от шоссе и
й—400 м от автобуса^ В каком направлении должен бежать
человек, чтобы выйти к какой-либо точке шоссе одновременно
с автобусом или раньше него? Человек может бежать
т скоростью е3= 4 м/с.
12. При какой наименьшей скорости человек (см. задачу
11) может встретить автобус? В каком направлении
должен при этом бежать человек? .
13. В данный момент автобус (см. задачу 11) находится
в точке А и движется по прямому шоссе АЕ. Найти геомет-
рическое место тех точек, где может находиться в настоящий
момейт человек, чтобы успеть сесть в автобус.-
14. Человек на лодке должен попасть из ‘точки А в
точку В, находящуюся на противоположном берегу реки
(рис. 3). Расстояние ВС=а. Ширина реки АС—b. С какой
наименьшей скоростью и относительно воды должна плыть
лодка, чтобы приплыть в В? Скорость течения реки оа.
15. Из пункта А , расположенного на берегу реки,
необходимо попасть в пункт В, двигаясь по прямой АВ
(рис. 4). Ширина реки АС— 1 км, расстояние ВС= 2 км,
максимальная скорость лодки-относительно воды ы=5 км/ч,
а скорость течения реки v—2 км/ч. Можно ли проплыть расстояние
АВ за 30 минут?
9 МЕХАНИКА.
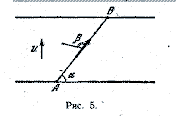
16. По реке из точки А в тетку В, находящуюся на
противоположтюм берету, вдоль прямой АВ, образующей
с линией берега угол а,
плывет катер (рис. 5). Под
прямым углом к берегу
дует ветер со скоростью а.
Флаг на мачте катера образует
угол Э с направлением
движения катера. Определить
скорость катера
относительно берега. Можно
л и поданным, приведенным
в условии задачи, определить скорость течения реки?
приведенным
в условии задачи, определить скорость течения реки?
1.7. По пересекающимся под углом а дорогам движутся
две автомашины с постоянными скоростями и v2. Определить
величину и направление скорости одного автомобиля
относительно другого. Через какое время после встречи
на перекрестке расстояние между машинами будет равно S?
18. Автомашины (см. задачу 17) не встретились на йе-
рекрестке, причем вторая машина проехала перекресток
на промежуток времени т позже первой. Каково было наименьшее
расстояние между автомашинами?
18. Две пересекающиеся прямые движутся поступательно
в разные стороны со скоростями щ и оа, перпендикулярными
соответствующим прямым. Угол между прямыми
равен а. Определить скорость точки пересечения прямых.
10 МЕХАНИКА.
Или смотрите в тексте для быстрого ознакомления (формулы отображаются не корректно).
Г л а в а I. МЕХАНИКА
§ 1. Кинематика равномерного прямолинейного
движения
1. В течение 1 часа после встречи лодки с ластами. лодка удалялась
от плотов. В течеиие 30 мин, когда мотор ремонтировался,
расстояние между лодкой и плотами не увеличивалось. Лодка догонит
плоты через 1 час, так как скорость ее относительно -воды,
а следовательно и относительно плотов, постоянна:
‘ o = S// = 7,5/(l + 0 ,5 + 1) = 3 км/ч.
2. Расстояние между электропоездами S=v t , с другой стороны,
S—vx-j-ит. Отсюда
u ^ v ( t—т)/т = 45 км/ч.
3. На рис. 266 AMN —графнк обычного.движения машины. CD —
график пути инженера до встречи с машиной в точке D. DB — график
движения машины после встречи с инженером. Согласно условиям
задачи BN = КМ =-10 мин. Время движения инженера до встречи
с машиной
СЕ = СМ — ЕМ = СМ — КМ/2 = 55 мин.
4. Так как время-оценивается ио последнему прибывшему, кратчайшим
оно будет тогда, когда все три туриста црйбудут одновременно.
163 МЕХАНИКА
График движения туристов изображен на рис. 267. Из него следует,
что движение пешком занимало у второго и третьего туристов одинаковое
время (Д//-)-Д/2), где Д/2—
время обратного движения велосипедиста.
Поэтому
МЛ<1+Д<*)+»аД*1 =
=^уср (Д*1 +
v2At1~ v 2At2 = v1 (Д^4-Д<2).
Отсюда средняя скорость туристов (
и С р —
ЗУ, Va , „
; 0ч70|9~-Х4-0, = 10 км/ч.
5. Графики одновременно, изображены
ломаными МЕВ и КЕА,где Е— точка
их встречи (рис. 268). Так как
скорость катеров относительно воды
одинакова, то МА и КВ — прямые
линии. Оба катера будут находиться
в пути одинаковое время, если они встретятся посередине между
пристанями. Точка их встречи О лежит на пересечении линии КВ
с перпендикуляром, восставленным из середины отрезка КМ. Графики
движения катеров изображаются линиями KOD и СОВ.
Как видно из рисунка, Д MAF & &COF, и, следовательно, искомое
время МС = 45мин.
6. Скорость катеров относительно воды vx и скорость реки и.г
определяются из уравнений S = / 1 (o1 -f-p2) и S = t2 (v1 — v2), где / х и
t t — время движения катеров по течению и против течения. Как
следует из условия, = 1,5 ч и / г = 3 ч. Отсюда
-S’ (71 —{— ^ 2
2 t \ t2 = 15 км/ч, v2— 2t it з = 5 км/ч.
Место встречи находится на расстоянии 20 км от пристани М.
7. Предположим, что река течет от С к Т со скоростью о0. Учитывая,
что время движения лодки и катера одинаково, можно
164 МЕХАНИКА
написать уравнение
\ t,2~bt’o v2—Vo.
где S — расстояние между пристанями. Отсюда
Но —f- «I- 4 v 2Vi — v2 = 0.
Следовательно,
о0 = —2о2 ± 4o1o2 = —20 ± 19,5 км/ч.
Решение o0 = —39,5 км/ч. следует отбросить, так как при этой скорости
реки ни лодка, ни катер не смогут подняться против течения.
Следовательно, v0 = —0,5 км/ч, т. е. река течет от пристани Т к пристани
С. ■
8. Расстояние R края тени от точки О, находящейся на земле
под фонарем, связано с расстоянием г человека от той же точки
соотношением R — jj—н ^ г. Следовательно, траектория тени подобна
траектории человека (центр подобия находится в точке О). Поэтому
вектор скорости края тени vT направлен так же, как вектор скорости
человека v, а по величине превосходит его в ^ раз (рис. 269).
9. Пусть за время At первая свеча сгорела на величину Ahb
а вторая свеча — на Дй2 (рис. 270). Тогда тень на левой стене (от
первой свечи) опустится на расстояние
Дх = Д -j-(Дйх — Д/г2) = 2Д hi — Ah2.
Тень на правой стене опустится на расстояние
Ay— A h2—(Д hi — Д h2) = 2Д h2—Д ft*.
Учитывая, что Дй1= -^ -Д /, Ah2~-^~ At, получим
1 1 1 2
J
165 МЕХАНИКА
t2 > t t , следовательно, ог > 0, a v% может быть величиной отрицательной,
т. е. на правой стене тень может перемещаться вверх.
10. Так как скорость движения в воде меньше скорости движения
по берегу, то путь АВ необязательно займет минимальное время.
Предположим, что траектория движения человека—ломаная линия
ADB (рис. 271). Необходимо определить, при каком значении х
время будет минимальным. Время движения t равно
f =
У’сР+х2 , S —х _ о 3 y’lP-j-x2 — OxX+OtS
VjV2
Это время будет минимальным, если у = о3 )Л12+ х 2—о,х будет иметь
наименьшее значение. Очевидно, что х, соответствующее минимальному
времени (, не зависит от расстояния S.
Для нахождения х, соответствующего минимальному значению у,
выразим х через у и получим квадратное уравнение
2l^i vtfP—У2 Q
Щ2 —V2i !—1>1
Решение его приводит к следующему выражению:
х —Viу ± Do у y2 + d2vl-^vld2
щ2 —v2i
Так как х не может быть комплексным, /то у2-\- d2v\ ^ v f d 2. Минимальное
значение у равно утт —dV^ о\—о |. Этому значению у соответствует
х = d v j y v\ — of. Если S < d v j f ^ of — of, то следует сразу
плыть по прямой А В к точке -В. В противном случае ладо пробежать
по берегу отрезок, равный A D ^ S —dvJ V of—of, а потом плыть к В.
Отметим, что для пути, соответствующего кратчайшему времени,
s in a = o r/o2.
И. Автобус находится в точке А, человек—в точке В (рис. 272).
Точка С—место встречи человека с автобусом, a —угол между направлением
на автобус и направлением, по которому должен бежать
человек, AC=?Vi<i. где t t н время движения автобуса
и человека до точки С,
166 МЕХАНИКА
Из & ABC видно, что: АС =Ъ sin a/sin % где sin fi=a/BC.
Следовательно, sin a==*^-Sli . По условию задачи /, ^ i2, поэтому
sin a ^ n o 1/to 2 = 0,6. Отсюда 3 6 ° 4 5 ‘< a < 143°15’.
Направления, по которым может двигаться человек, заключены
в пределах угла DBE. При движении вдоль BD или BE человек
Л J7 С 1 £
~Т~~
36°45^
Рис. 272. Р
достигнет шоссе одновременно с автобусом. В любую из точек шоссе,
находящуюся между точками D и Е, человек прибежит раньше
автобуса.
12. Наименьшую скорость можно определить из условий t 1 = / 2,
sin a=e£i1/bt>2 = 1. Отсюда = о.1 = 2 ,4 м/с. При этом a = 90°.
Следовательно, направление, по которому должен бежать человек,
перпендикулярно направлению на автобус. ю
13. В произвольную точку D шоссе автобус приходит за время
t = l/vi, где /—длина участка Л О шоссе. В эту же точку за время,
равное или меньшее t , человек может попасть, если он находится
в пределах круга радиусом г = о2/ с центром в точке D. Начертив
Рис. 273.
подобные круги для других точек, расположенных «а шоссе, получаем
искомую область. Границами ее являются две юбщие касательные
к окр’ужностям. -Угол а, который границы’составляют с шоссе,
определяется равенством sin a = г //= 02/0, (рис. 273).
14. Скорость лодки относительно берега v направлена на АВ
(рис. 274). Очевидно, v = v„ + u. Известны: направление вектора v
и величина и направление вектора v0. Вектор, и будет иметь минимальное
значение, как видно из чертежа, при uj_v. Следовательно,
“ m i n = yocosa, cos а = 6/ V»a24- 62.
15. Пусть скорость и направлена под углом а к берегу (рис. 275).
Тогда
(и cos a —о) т = ВС = а, (и si п а) т=ЛС ■= Ь}
166 МЕХАНИКА
где т — время движения лодки. Исключив а из этих уравнений,
будем иметь
(м2—о2) т2—2ш т—(a2-f-52)= 0 .
Отсюда т = 15/21 часа. Следовательно, преодолеть расстояние АВ за
30 минут невозможно. ‘
а а
В
Рис. 274. Рис. 275.
16. Пусть и0—скорость ветра относительно катера. Тогда
флаг на катере будет направлен вдоль и„. Если v — скорость катера
по. отношению к берегу, то u = u0+ v (рис. 276). В Д FCD Д DCF=
= p — f a—я/2, а Д FDC = я — р. По теореме синусов
sin ( а + Р — я/2) sin ( я—Р)’
s in ( a + p —я/2)
Следовательно, v = и (я —Р ) ‘ ®пРеделить скорость течения
реки по известной скорости катера относительно берега невозможно,
так как неизвестно направление движущегося катера относительно
воды.
17. Введем обозначения: и12— скорость второй автомашины относительно
первой, и21—скорость первой автомашины относительно
второй. Очевидно, «i2 = «2t и и?2 = of + t>2 -f- 2vtvs cos а (рис. 277).
Искомое время 1= S /« 12.
167 МЕХАНИКА
18. Примем момент проезда; перекрестка первой автомашиной за
начало отсчета времени. В системе координат, изображенной на
рис. 278, движение автомобилей описывается
уравнениями
х1 = — (и2 cos а) (, Уу = (vy sin а) t,
xa = —t>2T + ti2t, i/2 = 0.
Расстояние между автомашинами в любой
момент времени
S = V’ixy—x j 2+ ((/!—уг)2-
Отсюда
S2 = (of + + 2vyv2 cos a) t2 —
— 2v2 (vy cos а + н 3) тt + н ат2.
Найдя минимум квадратного трехчлена,
получим наименьшее расстояние: Smi„ =
— ^ 1 % sin а(см. решение задачи 17).
“ 12
19. За время Дt прямая АВ переместится на расстояние VyAt,
а прямая CD —на расстояние v2At. При этом точка пересечения
прямых перейдет в положение О’ (рис. 279). Перемещение 00′ точки
пересечения прямых найдется из треугольника OF О’ или 0Е0′, где
OF = VyAt!&\n ot = £ 0 ‘, ОЕ = v2At/ sin a = FO’:
00′ = y 0 F 2 + 0E2-{-20F-0E cos a = o At.
Отсюда
^ s l n a V vi + V2 + 2vi?2 cosa-.
169 МЕХАНИКА