ОТ МЕТРА ПО ПАРСЕКА

А. А. Михайлов

Страница переведена на новый сайт https://myeducation.su/ : страница

ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЖУРНАЛ Квант (6 июнь 1972)

Если хотите быстро ознакомится с содержанием статей, смотрите ниже.

Текст, для быстрого ознакомления (в тексте для быстрого ознакомления формулы могут отображаться не корректно):

Всем известно, что такое метр — мера длины, введенная при установ-
лении метрической системы мер Парижской академией наук в 1791 г.
во время великой французской революции.
Разнообразие мер, царившее до этого в разных странах, представляло
большие неудобства, особенно ощутимые при оживлении путешествий и
международной торговли. В связи с этим французские ученые предло-
жили основную меру длины заимствовать не от размеров человеческого
тела, а из неодушевленной природы, связав ее с размерами Земли как
планеты, в расчете на то, что величина Земли есть нечто неизменное.
Ведь именно это требуется от всякой меры. Поэтому было решено
принять за основную меру длины одну десятимиллионную часть рас-
стояния от полюса до экватора, точнее — четверти парижского мериди-
ана. Такая величина была выбрана в связи с тем, что часть этого мерк-
диана была измерена еще в начале XVIII века. Это измерение, произ-
веденное французскими учеными, дало неожиданный результат—длина од-
ного градуса меридиана оказалась не одинаковой в разных частях Зем-
ли, а слегка увеличивающейся с севера на юг. В таком случае Земля
не могла быть точным шаром, как раньше думали, а должна была быть
немного вытянутой в направлении полюсов, то есть по оси вращения.
Однако теоретические соображения Ньютона требовали обратного —
сплюснутости Земли у полюсов к растянутости к экватору. Это долж-
но быть следствием вращения Земли вокруг оси: точки на экваторе, на-
ходящиеся дальше от оси вращения и имеющие большую линейную ско-

рость, стремятся дальше удалиться от оси сращения, чем точки, находя-
щиеся ближе к полюсам. Ньютон показал, что Земля вследствие этого
должна принять форму эллипсоида, образованного вращением эллипса
вокруг малой оси. Большая ось эллипса—диаметр экватора Земли.
Вот тогда возник спор между учеными, основывавшимися на ре-
зультатах французского измерения меридиана, и теоретиками, разделяв-
шими мнение Ньютона. Для решения спорного вопроса французская академия наук снаря-
дила в тридцатых голах XVIII века две экспедиции для измерения дли-
ны градуса меридиана — одну на экватор в Перу и другую под северный
полярный круг в Лапландию (на границу нынешней Финляндии со Шве-
цией).
Результаты измерений, проведенных этими экспедициями, с несомнен-
ностью показали, что длина градуса меридиана у экватора заметно короче,
чем у полярного круга. Таким образом, прав оказался Ньютон: Зем-
ля имеет форму эллипсоидаю По более поздним уточненным из-
мерениям длина дуги 1° меридиана такова:
у полюса — 111 696 м,
у экватора — 110 576 м.
Что же касается размеров Земли, то, по одному из новейших опреде-
лений советского геодезиста ф. Н. Красовского,
радиус экватора а — 6378245 м,
полярный радиус b — — 6356863 ,w,
а — ь I
сжатие —— Но вернемся к концу XVIII века,
когда в дополнение к измерениям в

2 ОТ МЕТРА ПО ПАРСЕКА А. А. Михайлов 

Лапландии и Перу было закончено еще более точное градусное изме-
рение во Франции. Из всего этого материала была выведена длина ок-
ружности меридиана, одна сорока- миллионная доля которой и была принята за основную меру длины —
метр (что по-гречески означает «мера»).
Производя градусные измерения, французские ученые пользовались ста-
ринной мерой длины, называвшейся «туазом» (один туаз равнялся шести
парижским футам; фут — длина ступни; в одном футе было двадцать
дюймов: а дюйм — это мера длины, равная толщине большого пальца).
Определив длину метра, выраженную в долях туаза, изготовили плати-
новую линейку такой длины и по- ложили ее на вечное хранение в
Международном бюро мер в Париже. Эта линейка получила название «ар-
хивный метр» и стала законной мерой длины метрической системы, которую
приняли многие страны мира.
С тех пор много раз и в разных странах производились градусные из-
мерения, одно из которых, и самое замечательное, в 1816—1854 гг. было
проведено под руководством директора Пулковской обсерватории
В. Я- Струве и военного геодезиста К- И. Темпера. Это измерение охва-
тывало дугу в 25 протяженностью около 2800 км от рыбацкой дере-
вушки Фугленес на севере Норвегии до города Измаила на берегу Дуная.
Вычисленная по новейшим измере- ниям длина четверти меридиана ока-
залась несколько больше 10 миллионов архивных метров и составляет
10 002 138 м, так что архивный метр оказался примерно на 0,2 мм короче
своей номинальной длины. Однако менять уже принятую меру было не-
рационально, это вызвало бы лишь путаницу. Поэтому архивный метр
остался законной мерой длины, а для обеспечения ее сохранности были
сделаны 30 точных копий, которые распределили по разным странам. По-
стоянство этих «нормальных» метров периодически проверяется, для чего
их привозят в Париж, чтобы сравнить между собой и с архивным
метром. Точность измерений при сравнении достигает 0,0001 мм, то есть
доходит до 1/10 000 000 доли длины.
Американский физик Мяйкедьсон, а затем и другие сравнили длину
метра с длиной волны определенных линий оптического спектра и этим
закрепили его длину независимо от любых случайностей, которые могут
произойти с архивным метром или его копиями.
Такова вкратце история .метра, ставшего основной единицей длины
для всех измерений в повседневной жизни, науке и технике. Этот же
метр лежит в основе измерений расстояний в космосе, но пришлось прой-
ти сложный и длительный путь, прежде чем эту земную меру удалось пе-
ренести в космическое пространство, что было сделано в несколько эта-
пов.
Первым и важнейшим этаном было измерение расстояния от Земли до
Солнца. Необходимость начинать с этой величины вытекает из третьего
закона Кеплера. Он гласит, что квадраты времен обращения планет вок-
руг Солнца относятся как кубы их средник расстоянии от Солнца. Пе-
риоды обращения планет известны с очень большой точностью. Следо-
вательно, отношение кубов расстояний планет от Солнца тоже точно
известно, а для того, чтобы от отношений перейти к самим расстояниям,
нужно найти расстояние до Солнца от какой-либо одной планеты, напри-
мер, от Земли.
Попытки узнать это расстояние делались давно, еще до открытия за-
конов Кеплера в начале XV11 иска. Остроумный способ был предложен
в III веке до нашей эры греческим астрономом Аристархом Самосскнм,
правда, не для определения расстояния от Земли до Солнца, а для того,
чтобы узнать, во сколько раз Солнце or Земли дальше, чем Луна, которая
вследствие своего быстрого движения по звездному небу правильно счи-
талась ближайшим к нам небесным телом. Этот способ заключался в

3 ОТ МЕТРА ПО ПАРСЕКА А. А. Михайлов 

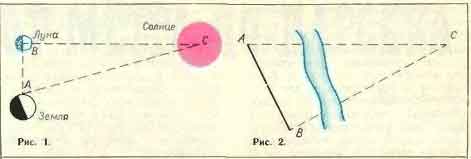
следующем. В первую и последнюю четверти диск Луны виден освещенным
ровно наполовину, и линия, отделяющая светлую сторону от темной,
представляется диаметром лунног диска (рис. 1). Угол между направле-
ниями Луна — Солнце и Луна — Земля (угол А ВС) прямой, как это
видно из рисунка 1. Если измерить в это время угол между направле-
ниями Земля —Луна и Земля —Солнце (угол ВАС), то можно найти от-
ношение расстояний Земля — Солнце и Земля — Луна (то есть отношение
-7^1. Во времена Аристарха Самосского для угла ВАС было получено
значение 87J. Следовательно, -го =sec 87°«#19. Так что Солнце оказа-
лось в 19 раз дальше Луны. Теперь мызнаем, что этот результат сильно
ошибочен и что Солнце почти в400 раз дальше Луны, так как угол
ВАС отличается от прямого угла всего лишь на 9′, a sec 89 51′ 382.
Измерения не могли быть выполнены с достаточной точностью, тем более,
что из-за неровностей поверхности Луны нельзя уловить момент, когда
освещена ровно половина ее диска.
Лить с усовершенствованием угломерных инструментов и примене-
нием оптических труб можно было попытаться измерить расстояния до
ближайших планет, а затем, пользуясь третьим законом Кеплера, вы-
числить расстояние до Солнца.
Для этой цели применяется геометрический простой метод засеч-
ки, которым широко пользуются и геодезисты и топографы при опреде-
лении расстояния до недоступного или удаленного предмета. Предста-
вим себе, что мы находимся в пункте А на берегу реки и нам нужно най-
ти расстояние до пункта С, находящегося на другой стороне реки фис.2).
Выбираем на «своем» берегу пункт В, расстояние до которого А В легко
измерить, и в треугольнике АСВ измерим углы CAB и СВА. Теперь
по известной стороне А В треугольника, называемой базисом, и двум
прилежащим углам можно вычислить расстояние АС. Это все простая ге-
ометрия, но для уверенного определения расстояния до пункта С
нужно, чтобы угол засечки АСВ не был слишком острым, то есть чтобы
базис А В не был очень малым по сравнению со сторонами АС и ВС.
Применительно к Солнцу этот способ крайне труден, так как самый
большой базис, который можно выбрать на Земле, — диаметр земного
шара — почти безнадежно мал по сравнению с расстоянием до Солнца.
Угол засечки в этом случае составляет всего лишь 17,6″.
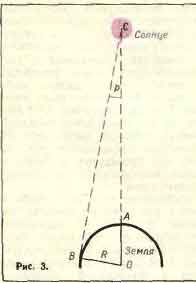
Для пояснения принципа определения расстояния до Солнца пред-
ставим себе двух наблюдателей на Земле (рис. 3). Одного в точке А,
из которой Солнце видно в зените (по тому же направлению, что и из
центра Земли О), и другого на экваторе в точке В; для него Солнце
находится на горизонте. Допустим, что каждый наблюдатель каким-ни-
будь способом определил направление на Солнце — соответственно АС

4 ОТ МЕТРА ПО ПАРСЕКА А. А. Михайлов

и ВС, которые пересекаются под очень
острым углом р. Тогда в прямоуголь-
ном треугольнике С ВО гипотенуза
СО равна
СО ^OBcosecp,
где ОВ — R — радиус земного шара.
Угол р называется параллаксом
Солнца. Очевидно, р — угол, под ко
торым из центра Солнца виден эк-
ваториальный радиус Земли. Его ве-
личина для среднего расстояния до
Солнца равна 8,8″. Считая R —
— 6400 км, получаем
СО = 6400-cosec 8,8″^
ъ 150 000 000 км.
Таково приближенное среднее зна-
чение расстояния до Солнца. Это имен-
но среднее значение, так как земная
орбита есть эллипс и Солнце находит-
ся не в его центре, а в фокусе; поэтому
расстояние до Солнца в течение года
изменяется примерно на 1,7% =
= 2 550 000 км в ту и другую сто-
рону.
Мы привели эти рассуждения толь-
ко для того, чтобы показать принцип
определения среднего расстояния меж-
ду центрами Земли и Солнца. Это рас-

расстояние называют астрономической
единицей длины или сокращенно а.е.
Астрономическая единица является
основной мерой для определения всех
расстояний в солнечной и в звездной
системах.
Трудность в практическом выпол-
нении описанных измерений заключа-
ется в определении направлений АС
и ВС. Действительно, по отношению
к чему можно находить эти направ-
ления? Если бы днем вокруг Солнца
на небе были видны звезды, они
дали бы тот далекий фон, по отноше-
нию к которому можно определить эти
направления. По этого нет, к тому
же и центр Солнца ничем не обозна-
чен, так что визировать его непо-
средственно нельзя. Вот почему удоб-
нее определять расстояние до пла-
неты, которая видна ночью на фоне
звезд. (Есть планеты, которые зна-
чительно ближр к Земле, чем Солнце,
что облегчает измерения.)
Первоначально для этой цели был
выбран Марс, наблюдения которого в
1672 году впервые дали более менее
верное значение параллакса Марса;
а зная его, как мы уже упомянули,
можно было вывести и параллакс
Солнца. Когда в начале прошлого
века были открыты первые малые
планеты, появилась возможность поль-
зоваться ими, так как некоторые из
них подходили особенно близко к
Земле. Кроме того, они малы по
размерам и видны на небе как точки,
подобно звездам, что сильно облег-
чает определение направлений. Од-
на из таких планет — Эрос — в
1930—31 гг. приближалась до рас-
стояния в 0,15 а. е., когда ее парал-
лакс достигал 60″. Тогда наблюде-
ниями ее занимались 26 обсерваторий
разных стран. Обработка получен-
ного огромного материала дала на-
иболее точное значение солнечного
параллакса. Тем не менее рассчитан-
ная по нему длина а. е. все же со-
держала ошибку порядка 50 000 км.
Эта ошибка может показаться очень
большой. Однако нужно учесть, к
какому огромному расстоянию она
относится и насколько трудно

5 ОТ МЕТРА ПО ПАРСЕКА А. А. Михайлов

измерять параллакс. Такую ошибку
можно проиллюстрировать следую-
щим образом. Представьте себе, что
вы измеряете ширину комнаты и на-
ходите, что она равна 3 м. Нелегко
вам будет получить при этом ошибку,
не превосходящую 1 мм. Но именно
такую относительную величину пред-
ставляет ошибка 50 000 км по срав-
нению с а. е. в 150 000 000 км.
Для большинства случаев в астро-
номии такая точность в определении
длины а. е. была достаточной. Но с
началом космического века потре-
бовалась значительно большая точ-
ность. Действительно, космические ра-
кеты запускались к Венере и к Марсу.
Диаметры этих планет соответственно
равны 12 400 км и 6800 км. Поэтому
для корректировки полета ракеты так,
чтобы она попала в заданное место
планеты, нужно знать а. е. с точ-
ностью по крайней мере в десять раз
большей. Здесь на помощь пришла
радиолокация. Регистрация отражен-
ного планетой сильного импульса ра-
диоволн и определение времени про-
хождения сигналом расстояния туда
и обратно позволили вычислить рас-
стояние до планеты, а вместе с тем
и а. е. с точностью до нескольких
сотен километров, то есть повысить
точность в сотни раз. Такие наблю
дения были проведены в СССР и
США и дали очень согласные резуль-
таты. С небольшим округлением а. е.
теперь принята равной 149 600 000 км.
Это и есть основная единица дли-
ны, которой измеряются расстояния
во вселенной, как в солнечной си-
стеме, так и за ее пределами. Однако
Д1Я выражения расстояния до звезд
эта единица все же слишком мала,
и здесь употребляется другая, го-
раздо большая мера (ведь не станем
же мы мерить расстояние между го-
родами миллиметрами). Такая ук-
рупненная мера равна 206 265 а. е.,
или 3,0857-1013 км, и называется
парсеком. Выбор такого странного со-
отношения между а. е. и парсеком
будет понятен из следующего.
Расстояния до звезд, по крайней
мере ближайших к нам, измеряются
тем же геометрическим способом за-
сечки, что и расстояния до ближай-
ших планет. Но вследствие чрезвы-
чайной удаленности звезд находя-
щийся в пределах земного шара ба-
зис, едва достаточный для измерения
расстояний до планет, исчезающе мал
по сравнению с расстоянием до звезд.
Здесь нужен базис во много раз более
длинный. И такой базис нашли.
Через каждые полгода Земля, пе-
реходя на противоположную точку
своей орбиты, смещается почти на
две а. е., то есть 300 000 000 км от
1ервоначального положения. Такое
смещение должно вызвать изменение
направления, по которому с Земли
видна та или иная звезда, причем
чем ближе звезда, тем больше долж-
но быть это изменение. Звезды должны
казаться смещающимися и качаться
из стороны в сторону, что является
отражением орбитального движения
Земли вокруг Солнца. Угол, на ко-
торый смещается звезда при пере-
мещении Земли на одну а. е., назы-
вается годичным параллаксом звез-
ды.
Существование такого видимого по-
качивания звезд с годичным периодом
было впервые теоретически предска-
зано Коперником в XVI веке и
должно было служить наиболее вес-
ким доказательством движения Земли.
Однако наблюдения того времени
не обнаруживали ничего подобного.
По Коперник, убежденный в пра-
вильности своей теории, утверждал,
что звезды слишком далеки, чтобы
их параллаксы можно было изме-
рить. Тихо Браге в конце XVI века
тоже не мог обнаружить параллак-
тических смещений звезд, хотя его
наблюдения превосходили по точ-
ности все предыдущие и были на
пределе возможностей для- невоору-
женного глаза.
Изобретение зрительной трубы в
десятки раз повысило точность из-
мерений. Тем не менее, параллаксы
звезд оставались незаметными. Лишь
в 1837—38 гг. три выдающихся астро-
нома: В. Я- Струве в Дерпте (ныне
Тарту в Эстонии), Ф. Бессель в

6 ОТ МЕТРА ПО ПАРСЕКА А. А. Михайлов

Кенигсберге (ныне Калининграде) и
Т. Гендерсон в обсерватории Мыса
Доброй Надежды обнаружили м из-
мерили параллаксы трех звезд: яр-
кой Веги в созвездии Лиры, довольно
слабой, но обладающей большим соб-
ственным движением 61-й звезды со-
звездия Лебедя и яркой звезды юж-
ного неба, невидимой в наших ши-
ротах — альфа Центавра. Парал-
лаксы всех этих звезд оказались
меньше 1″.
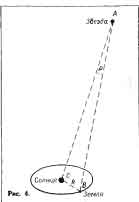
Дадим теперь определение годич-
ного параллакса звезды (рис. 4):
это есть угол р, под которым со звез-
ды А был бы виден радиус земной ор-
биты R = ВС (если считать ор-
биту окружностью).
Из прямоугольного треугольника
ABC найдем расстояние D =¦¦ В А
от Земли до Звезды (радиус Земной
орбиты в среднем равен 1 а. е.):
sinp smp
Если выражать р секундами дуги,
то так как этот угол очень мал. можно
считать, что
sin/? сь /? (в долях радиана).
В окружности единичного радиуса,

длина которой 2л, содержится
360-60-60 — 1 296 000 секунд, откуда
2л 1
доли радиана.
J 2% ооо
Тогда D
206 2(й
а. е.
Вот откуда взялось это странное
на первый взгляд число. 206 265 а. с.
и является новой единицей длины
для измерения звездных расстояний.
Очевидно, это есть расстояние до
воображаемой звезды, параллакс ко-
торой равен одной секунде, откуда и
произошло само название парсек (со-
кращенно пс), составленное из пер-
вых слогов слов «параллакс» и «се-
кунда». Расстояние же до звезды с
параллаксом в р» выражается те-
перь очень просто:
I
D—
пс
Звезд с параллаксом, равным 1″,
мы не знаем. Все звезды находятся
дальше, так что р всегда есть пра-
вильная дробь. Ближайшая извест-
ная звезда — альфа Центавра — име-
ет параллакс 0,75″, и расстояние до
нее равно г-=г„ -¦= I.33 пс. Наиболее
яркая звезда неба Сириус находится
в два раза дальше.
Выразим расстояние в один пар-
сек в километрах:
1 яс = 1 а. е.-206265^3,0857-10»кя.
Следовательно, расстояние до бли-
жайшей к нам звезды альфа Цен-
тавра равно примерно 4-Ю13 к,«.
Звезд с параллаксом больше 0,1″,
то есть находящихся на расстояниях,
меньших 10 пс, очень мало, всего
несколько десятков. Огромное боль-
шинство звезд гораздо дальше, они
отстоят от нас на сотни и тысячи пар-
секов. Для таких расстояний упот-
ребляется единица длины кило-
парсек, в тысячу раз большая пар-
сека.
Итак, мы рассказали о длинном
пути от земной единицы длины —
метра — до парсека, которым изме-
ряются расстояния до звезд других

7 ОТ МЕТРА ПО ПАРСЕКА А. А. Михайлов

звездных систем. В популярной
литературе часто употребляется дру-
гая единица — световой год, то есть
расстояние, которое луч света в ва-
кууме проходит в течение одного
года. По наиболее точным опре-
делениям скорость света равна
299 792Ь, 5кл/с; число секунд в кален-
дарном годе C65,25 суток) есть
365,25 • 24 • 60 • 60 = 31 557 600. Пе-
ремножив эти числа, мы получим,
что световой год равен 9,46-1012 км.
Это огромное число все же меньше
одного парсека: 1 пс — 3,26 све-
товых лет. Ближайшая к нам звезда
альфа Центавра находится на рас-
стоянии 4,35 световых лет, а от бли-
жайшей внегалактической туман-
ности в созвездии Андромеды свет
идет примерно 1 500 000 лет, и рас-
стояние до нее оценивается в
460 000 парсек, или 460 килопарсек.
Для определения таких больших
расстояний геометрический способ за-
сечки совершенно непригоден. По-
этому были найдены другие, астрофи-
зические способы, основанные на оп-
ределении светимости звезд.
Иногда большие числа называют
астрономическими.
Приведенные примеры оправдыва-
ют это название.

8 ОТ МЕТРА ПО ПАРСЕКА А. А. Михайлов

 

ОТ МЕТРА ПО ПАРСЕКА