Потенциальная энергия тел в поле тяготения. Н.М.СПЕРАНСКИЙ
Если хотите быстро ознакомится только с содержанием статей, смотрите ниже.
Текст, для быстрого ознакомления (в тексте для быстрого ознакомления формулы могут отображаться не корректно):
Страница переведена на новый сайт https://myeducation.su/ : страница
ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЖУРНАЛ Квант (6 июнь 1972)
Потенциальная энергия тел в поле тяготения
Н.М.СПЕРАНСКИЙ
Еще в школьном курсе физики
указывается на существование глу-
бокой аналогии между гравитацион-
ным и электростатическим полями,
вытекающей из формального матема-
тического сходства закона тяготения
Ньютона и закона Кулона. И в поле
тяготения и в электростатическом
поле работа по перемещению тел или
электрических зарядов не зависит от
формы пути, а определяется лишь по-
тенциалами точек начала и конца пе-
ремещений и величинами масс или
зарядов. Отсюда, в свою очередь,
следует, что работа по замкнутому
контуру, как в том, так и в другом
поле равна нулю.
Потенциал любой точки элек-
kQ
тростати чес кого поля <р =
где Q — точечный заряд, образовав-
ший поле, г — расстояние от данного
заряда до точки, в которой определя-
ется потенциал ф, a k — постоянная,
зависящая от выбора системы единиц.
В системе СГС k ¦ 1; в системе СИ
k— ; ft- коэффициент пропор-
циональности в законе Кулона.
Работа по перемещению точечного
заряда q равна
(I)
где г, соответствует начальной точке,
в которой находился заряд q, a
г2 — его конечному положению.
Из аналогии между гравитацион-
ным и электрическим полем заклю-
чаем, что работа W в гравитационном
поле, например, Земли равна
20
где у — гравитационная постоянная
(коэффициент пропорциональности в
законе тяготения), М — масса Земли,
т — масса точечного тела, переноси-
мого в поле силы тяготения Земли,
a гх и г, — соответственно началь-
ное и конечное расстояния от данного
тела до центра планеты.
Мы поставили в этой формуле знак
«—», так как два тела всегда притя-
гиваются. Это соответствует взаимо-
действию положительного и отри-
цательного зарядов. Для того чтобы
увеличить расстояние между телами
(г., > г,), нужно совершить положи-
тельную работу. При уменьшении
расстояния между телами направление
перемещения тела совпадает с направ-
лением действующей на него силы.
Следовательно, в этом случае работа
отрицательна.
Определим теперь потенциальную
энергию тела на расстоянии R от
центра Земли. Так как изменение
потенциальной энергии равно работе,
затрачиваемой на перемещение тела,
то, полагая, что потенциальная энер-
гия равна нулю бесконечно далеко
от Земли (г, = оо), найдем
* — -«(»
График зависимости U от рас-
стояния R показан на рисунке 1.
Это гипербола, изображенная сплош-
ной красней линией. На поверхности
Земли U = —к-tn, где Яз —радиус
Земли. *3
Обычно решая задачи, связанные
с перемещением тела у поверхности
Земли, мы пользуемся другой фор-
мулой:
U = mgh,
20 Потенциальная энергия тел в поле тяготения
где h — расстоянгк; до поверхности
Земли и ?—ускорение свободного
падения. Не ошибаемся ли мы?
Давайте отсчитывать величину по-
тенциальной энергии тела от поверх-
ности Земли, то есть считать, что на
поверхности Земли потенциальная
энергия равна нулю. Это означает,
что нам нужно поднять красную кри-
вую на рисунке 1 на^-ш, а форму-
лу для потенциальной энергии тела
записывать так:
U — _ ~ т 4- тг~1П = у Mm ± ±L
к Цз RR3
Если изменение расстояния тела
до центра Земли h = R — R3 мало
Рис. 1.
по сравнению с У?з
^ R\. Поэтому
то /? «=; /fe и
Поскольку в большинстве практиче-
ских задач вращением Земли обыч-
но пренебрегают, можно считать,
что на поверхности Земли тело мас-
сы пг притягивается с силой
уМт уМ
~ 0 то -Ц- — 0 и U — теп.
К3 К3
Мы снова получили ту же формулу.
Ясно, что ею можно пользоваться при
h<^Rs. При этом мы заменяем пунк-
тирную кривую касательной к ней в
точке R = R3 .
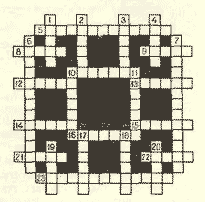
Кроссворд МФТИ
В № I нашего журнала
за 1972 год мы поместили
кроссворд МФТИ (кстати, как
заметили многие наши чита-
тели, в ответах на этот
кроссворд есть неточность:
«фокус о светом» — это,
конечно, «преставление»,
а не «представление»).
Предлагаем вам еще раз
проверить свои «юмористи-
ческие способности». Мы
уверены, что »ы справитесь
с помещенным ниже крос-
свордом. Если захотите (на
всякий случай) проверить,
верно ли вы ответили на все
вопросы кроссворда,’ то по-
смотрите на стр. 58 этого
номера «журнала.
По вертикали:
1. Приспособление для выращивания
молодежи. 2. Твердая еда. 3. Съедобный
эллипсоид. 4. Коммунальный чайник без
ручки. 6. Действие, обратное вымогатель-
ству. 7. Псевдоним. 10. Первое русское де-
кольтированное платье. 11. Место прописки
Адама Козлевича. 17. Клятва наших пред-
ков. 18. Геометрическое место равных
топов. 19. Пять шестых восточного бандита.
20. Намело пресловутого танца.
По горизонтали:
5. Черт зиает что. 8. Комета без голо-
вы. 9. Папирус двадцатого века. 10. Насе-
ленный пункт в окрестностях Долгопруд-
ного. 12. Инородный подкожный предмет.
13. Ликвидация брака. 14 То, что думает
волк-интеллигент, глядя на Красную Ша
почку. 15. Сельскохозяйственный работник.
16, Фотополуфабрикат. 21. Организованная
паника. 22. Национальное сухое блюдо.
23. Ругательство.
21 Потенциальная энергия тел в поле тяготения