Работа и энергия

§ 7. Работа и энергия.

Страницы переведены на новый сайт:
СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ
https://myeducation.su/sbornik-zadach-po-elementarnoj-fizike/

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Опыт Герике с «Магдебургекими полушариями»
состоял в том, что две медные полусферы плотно соедини-

ЗАДАЧИ ПО ФИЗИКЕ.
Свойства пара.

36 СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ. Работа и энергия. 

лись основаниями и из получившегося долото шара выкачивался
воздух. Атмосферное давление настолько плотно
* прижимало полушария друг к другу, что их могл.и разъединить
только с помощью нескольких лошадей. Определить,
, сколько лошадей нужно для отрыва полушарий, если каждая
лошадь тянет с силой F? Радиус полусферы R, атмосферное
давление равно р.
157. Как объяснить тот факт, что при падении камня на
Землю изменение количества движения Земли равно изменению
количества движения камня, а изменение кинетической
анергии Земли не учитывается? ^
158. Сваю массой в 100 кг забивают в грунт копром, масса
которого 400 кг. Копер свободно падает с высоты 5 м,
и при каждом его ударе свая опускается на глубину 5 см.
Определить силу сопротивления грунта, считая ее постоянной.
159. Ящик с песком, имеющий массу М, подвешен на
тросе длины L. Длина троса значительно больше линейных
размеров ящика. Пуля, масса которой т, летит в горизонтальном
направлении, попадает в ящик и застревает в нем.
Трос после-попадания пули отклоняется на угол а от вертикали.
Определить скорость пули.
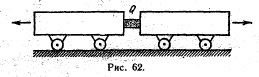
160. Две тележки с зак пшёнными колесами расталкиваются
взрывом заряда Q помещенного между ними (рис.62).

Тележка массой 100 г проходит путь 18 м и останавливается.
Какой путь пройдет вторая тележка массой 300 г.? Коэффициент
трения между землей и тележками равен А.
161. Решить задачу 101, применяя закон сохранения количества
движения и рассматривая изменение кинетической
энергии тележки и тела.
162. Ракета взлетает вертикально вверх, выбрасывая
раскаленные газы последовательно двумя равными пор-
. циями. Скорость истечения газов относитедьно ракеты постоянна
и равна и. Каким должен быть промежуток времени
между сгоранием порций, чтобы ракета достигла максимальной
высоты? Сгорание топлива происходит мгновенно.
Сопротивлением воздуха пренебречь.

37 СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ. Работа и энергия.

163. Горючее ракеты сгорает равными порциями массы
т. Сгорание происходит мгновенно. Будет ли скорость
истечения газов относительно ракеты постоянна, если при
сгорании каждой порции механическая энергия системы
меняется на одинаковую величину?
164. Тело поднимают на вершину горы один раз по
пути ADC’и другой раз — по ABC (рис. 63). Доказать, что
при медленном подъеме совершенная
работа будет одной и
той же, если коэффициент трения
на обоих склонах одинаков,
165. Какую силу следует
приложить к рукоятке винтового
домкрата, чтобы удержать
в равновесии поднятый домкратом
груз Р? Шаг винта равен А,
длина рукоятки R. Трение отсутствует.
166. Найти максимальный
Рис- 63. коэффициент полезного действия
винтового домкрата, у которого
силы трения не позволяют грузу опускаться.
167. К корзине воздушного шара массы М привязана
веревочная лестница длины /, на конце которой стоит человек
массы т. Вся система находится в воздухе в положении
равновесия. Определить, какую работу должен совершить
человек, чтобы подняться в корзину. Какова будет скорость
воздушного шара, если человек перемещается по лестнице
со скоростью v относительно нее?
168. Как должна измениться мощность мотора насоса,
чтобы он стал перегонять через узкое отверстие вдвое боль- ■
шее количество воды в единицу времени?
169. Прямоугольная яма, площадь основания которой
S и глубйна Я, наполовину заполнена водой. Насос выкачивает
воду и подает ее на поверхность земли через цилиндрическую
трубу радиуса R.
1) Какую работу совершил насос, если он выкачал всю
воду за время т?
2) Какую работу совершил насос за то же время, если
на дне ямы лежит каменная плита прямоугольной формы,
площадь основания которой S t и высота А? (Глубина воды
в яме по-прежнему равна Я/2.)
179. Какую работу нужно совершить, чтобы за время
т подняться по движущемуся вниз эскалатору метро? Вы-

38 СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ. Работа и энергия.

сота подъема h, скорость эскалатора постоянна и равна v,
угол наклона эскалатора к горизонту а.
171. Берем пружину за среднюю точку О и оттягиваем
на расстояние л; (рис. 64), а затем отпускаем. Пружина быстро
становится растянутой равномерно, причем переход к
этому состоянию сопровождается некоторой потерей энергии.
Оценить ее, считая Жесткость k пружины очень большой.
(После того, как пружина станет растянутой равномерно,
возникнут колебания груза т, сопровождающиеся
дополнительными потерями энергии.)

172. В вагоне равномерно движущегося поезда стоит
человек, растягивающий пружину с силой F (ряс. 65). Поезд
прошел путь L. Какую работу совершит человек в системе
координат, связанной с Землей?
173. В вагоне равномерно движущегося поезда человек
растянул пружину, прикрепленную к передней стенке вагона,
на длину /. За это время поезд прошел путь L. Какую
работу совершил человек в системе координат, связанной с
Землей? Чему равна эта работа в системе, связанной с поездом?
Растягивая пружину, человек идет против движения
поезда.
174. Происходит соударение двух абсолютно упругих
шаров, массы которых равны тх и т%. Начальные скорости
шаров щ и оа. Найти скорости шаров после удара. Удар
считать центральным: скорости шаров направлены вдоль
линии, соединяющей их центры. Проанализировать два
случая: 1) скорость второго шара до удара равна нулю;
2) массы шаров равны.
175. Происходит соударение двух абсолютно упругих
шаров, массы которых равны mt н « а. Начальные скорости
шаров vx и о*. Удар центральный. Определить максимальную
энергию упругой деформации.

39

176. На абсолютно гладкой горизонтальной плоскости
покоятся два упругих бруска равной массы т, скрепленных
пружиной длины /(рис. 66). Коэффициент упругости пружины
равен k. На один из брусков, например на левый, налетает
со скоростью v третий брусок, имеющий также
т гг 777 777
-т ь —
77/7////777777///77/У77//7?уУ7У/777У7У7//777/////777/7////л
Рис. 66.
массу т. Показать, что связанные пружиной бруски всегда
будут двигаться в одну сторону. Определить скорости брусков
в момент, когда пружина максимально растянута.
177. Две пластинки,массы которых равны/«.скреплены
пружиной с коэффициентом жесткости k (рис. 67). Верхнюю
пластинку опустили настолько, что деформация пружины
стала равной х, и затем р)тус^и.»£^№деяи«ь,,’на какую
высоту пбднйметсяпосле этого центр масс системы.
гг
W//’У/^/У/У//M/7/777/////}л////S,
Рис. 67. Рис. 68.
178. Шарик, движущийся со скоростью v, налетает на
стенку, которая движется навстречу шарику со скоростью
и (рис. 68). Происходит упругий удар. Определить скорость
шарика после удара. За счет чего изменяется кинетическая
энергия шарика? Массу стенки считать бесконечно
большой.
179. С высоты А=73,5 м сбрасывают два одинаковых по
массе камня, связанных веревкой, дайна которой 7=39,2 м.
Первый камень начинает падать на т = 2 с раньше второго.
Через какое время после начала падения камни упадут на
землю? Падение происходит без начальной скорости. Рассмотреть
два случая: 1) веревка абсолютно упругая;
2) веревка абсолютно неупругая.
189. Несколько одинаковых упругих шаров так подвешены
рядом на нитях равной длины (рис. 69), что расстоя

40

ния между соседними шарами очень малы, Как будут вести
себя шары, если отклонить крайний шар и отпустить,
отклонить одновременно
два шара, отклонить три
шара и т. д.?
181. На плоскости лежат
в ряд (с небольшими
промежутками) шарики
одинакового размера (рис.
70). Один из средних шариков
сделан из стали, остальные
— из слоновой кости
(масса стального шарика
больше), На шарики
справа вдоль линии центров налетает костяной шарик (той
же массы). Как будут двигаться шарики после удара?
Рис. 69.
182. На концах очень длинной нити подвешены равные
грузы массы т (рис. 71). Нить перекинута через два малых
Неподвижных блока, расположенных на расстоянии 21
друг от друга. Найти скорости грузов по истечении достаточно
большого промежутка времени, если к середине нити
прикреплен груз массы 2т.
Рис. 71.
188. Груз массой 536 г, удерживаемый первоначально
у потолка посередине между точками А и В, начинает

41

опускаться вниз (рис. 72). При каком значении угла A N В
его скорость по абсолютной величине станет равной скорости
груза массы тг= 1000 г? Как будут двигаться грузы
в дальнейшем?
184. На двух катках разных радиусов лежит тяжелая
доска, образующая угол а с горизонтом. Определить, как
будет двигаться доска. Проскальзывание отсутствует. Массой
катков пренебречь.
185. Однородная цепочка длины 21 и массы М лежит на
абсолютно гладкой доске. Небольшая часть цепочки пропущена
в отверстие, сделанное в доске (рис. 73). В начальный
момент времени лежащий на доске конец цепочки
С
Рис.,73.
придерживают, а затем отпускают, и цепочка начинает соскальзывать
с доски под действием силы тяжести свешивающегося
конца. Определить скорость движения цепочки в
тот момент, когда длина свешивающейся части будет равна
Определить для того же момента времени ускорение
цепочки я реакцию края доски.
186. Тележка массы М может двигаться без трения по-
горизонтальным рельсам. На тележке укреплен математический
маятник (шарик массы
т, подвешенный на нити
— длиной /) (рис. 74). В начальный
момент времени тележка
и маятник покоились, и нить
. . . . отклонили на угол а <эт верти-
кали. Какова скорость тележки
в тот момент, когда нить
Рис- 74- маятника будет составлять с
вертикалью угол Рф < а )?
187. Клин, масса которого М , находится на абсолютно
гладкой горизонтальной плоскости. На клине лежит брусок
массы т. Брусок под действием силы тяжести может
скользить по клину без трения. Считая, что в начальный момент
времени система находилась в покое, определить скорость
клина в тот момент времени, когда брусок опустится
по вертикали на высоту ft.

42

188. Стержень, закрепленный
между двумя муфтами,
может свободно перемещаться
в вертикальном направлении Ш ИИ
(рис. 75). Нижний конец стер- т .
жня отирается на гладкий’
клин, лежащий на гори-
зонтальной плоскости. Масса щ
.стержня /п, клина М. Трение
отсутствует. В начальный мо-
мент стержень и клин покоились.
Определить: скорость
и клина в момент, когда стержень
опустится на высоту h; скорость моти стержня относительно
движущегося клина; ускорение а стержня,

43 СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ. Работа и энергия.

§ 7. Работа и энергия. Ответы.

 

155. Работа силы не зависит: от массы’того тела, на которое действует
данная сила. Сила в 30 Н совершит работу A = F h— 150 Дж.
Эта работа пойдет на увеличение потенциальной энергии (50 Дж) и
кинетической энергии (100 Дж) груза.
156. Прежде всего нужно найти силу давления воздуха на одно
из полушарий. Представим себе, что его основание закрыто плоской
крышкой—диском радиуса R. Тогда, если из получившегося сосуда
откачать воздух, сила давления на плоскую крышку будет F2 = pS =
= pitRK Очевидно, такова же будет и сила давления воздуха на
полушарие; В противном случае силы взаимно не уравновесятся и
сосуд должен будет вечно’двигаться в сторону большей силы. Число
лошадей должно быть равно Fi/F, так как-другое полушарие1 может
быть просто привязано к. столбу. Натянутая веревка создаст точно
такую же силу, как и упряжка лошадей, тянущая с другой стороны.
157. Изменение количества движения тела равно импульсу силы
тяжести. Так как силы, действующие на- камень и Землю, равны и
действуют одинаковое время, то. равны и изменениям количества движения
этик тел; Изменение кинетической1 энергии тела равно» работе
сил тяготения. Силы-равны, но пути; пройденные камнем и Землей;
обратно пропорциональны изгмассам: Именно поэтому закон сохранения
энергии можно записать в форме; не учитывающей изменения
кинетической.энергии Земли: const, где/л—масса камня;
a W — потенциальная энергия взаимодействия.
158. По закону сохранения энергии m1gA=m14«/2, где т1—’
масса копра, Н—высота падения копра, v1—скорость копра перед
ударом. Ввиду кратковременности удара сила сопротивления, не может
заметно изменить общего количества движения системы. Так как
удар неупругий, то m1a1=(OTi+m2)t>2, где гщ— масса сваи* н2 —
скорость копра и сваи1 в первый момент после-удара; Механическая
энергия копра и сваи расходуется на работу против силы, сопротивления
грунта F:
где S—глубина погружения сваи в грунт; Отсюда

214 СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ. Работа и энергия.. Ответы.

159. В результате неупругого удара линейная скорость ящика
с находящей. ся.вашм-дулей, в первый м» омент б, удет равна r rmf ;v— Ш
где о—скорость пули. Угол отклонения « на основании закона сохранения
энергии связан со скоростью » соотношением
Отсюда
(М4-т)иг m V . . . , .
2 ^ 2 Щ + ^ Г {М +т )1 {1~ йа&а)й-
ti==2_ si. nr-аr М-\—-т 1лг/тf—~ 2 т
160.‘Ввиду кратковременности взрыва внешние горизонтальные
силы (силы трения) не могут за время взрыва заметно изменить
общего количества движения системы. До взрыва и сразу после -него
оно остается равным нулю. Следовательно, m1o1-f-/n2o2= 0 . Отсюда
»,/»2= —т^Шх. Так как тележки в конце концов останавливаются,
их начальные кинетические энергии тратятся на -работу против .сил
трения:
‘ ‘14*^2=^
Отсюда o*/o|=S1/Sa, и, следовательно, S * » 2 м.
161. Обозначим через и скорость тела и тележки после прекращения
их относительного движения. На основании закона сохранения
количества движения
(Л !-|-т )и =Л 1вв. (1)
Тележка теряет «яяетическую энергию ввиду того, что сила трения /,
действующая на тележку, совершает отрицательную работу: Mvy2 —
— Mu2/2= fS , где S—путь, пройденный тележкой. Тело приобретает
кинетическую энергию за счет того, что сила трения, действующая
на тело, совершает положительную работу: mu?/2 — fs. Здесь s—путь,
пройденный телом.
Изменение кинетической энергии системы
Ale* Г Л1иа . тиг1
— 2- “ L ~ + “ J
= / ( S — s ) , (2)
как легко видеть, равняется силе трения, умноженной на относительное
перемещение тела вдоль тележки. Из уравнений (1) и (2) сле-
mMv* mMv\
дует, что S — * = 2f (M + m) • Так как S — s < / , то
Мо®
Учитывая, что f = kmg, получаем I Э» 2feg (М+т) ‘
162. В результате сгорания второй «порции топлива скорость о
ракеты увеличится на величину До. По закону сохранения количества
движения (так как сгорание ‘происходит мгновенно)
(А1-}-«)в= М (о+ До)-f-т (о— и),
где т —масса порции топлива, М—.масса ракеты без топлива, и —
скорость истечения газов относительно ракеты. Приращение скорости

215

ракеты Av=-^- и не зйвисит от скорости v ракеты перед сжиганием
второй порции. Напротив, приращение кинетической энергии ракеты
(без топлива)
М(о+Дн)2 МФ ( т \
Д Д .= — V — — — г — = ти
будет тем больше, чем больше v.
Высота подъема ракеты определяется полученной ею энергией.
Поэтому вторую порцию топлива выгоднее сжечь в момент, когда
скорость ракеты наибольшая, т. е. непосредственно вслед за первой
порцией. При этом наибольшая часть механической энергии, возникающей
при сгорании топлива, будет сообщена ракете, а механическая
энергия продуктов сгорания минимальна.
163. Достаточно рассмотреть последовательное сгорание двух
порций топлива. Пусть вначале масса ракеты с топливом равна
М -f- 2т. После сгорания первой порции скорость ракеты v =
= m«j/(M+m), Где и1—скорость газов относительно ракеты. Начальная
скорость ракеты принимается равной нулю. Приращение скорости
ракеты после сгорания второй порции Av=mu2/M, где иг —
новое значение скорости газов относительно ракеты.
При сгорании первой порции выделилась механическая энергия
АЕ1 = (М-\-т) оа/2 + яш|/2. При сгорании второй порции выделяется
энергия
Л1(»+Дц)* т(о—и2)2 (М-\-т)Ф
Д £ а 2 Н 2 2 •
По условию задачи АЕ1=АЕ2. Отсюда
о / от2 , т \ 2 ( т2 . т \
1 \2 (M + m ) ‘ ^ 2 ) ~ U* \ 2 M ^ ~ 2 j ‘
Следовательно, > ца—скорость газов относительно ракеты уменьшается.
Это связано с уменьшением массы ракеты в процессе сгорания
топлива.
164. Оба склона можно разбить на множество сколь угодно малых
наклонных плоскостей с различными углами наклона. Рассмотрим
одну из них (рис. 346). Работа по подъему тела на такой наклонной
плоскости равна работе против сил тяжести mg АН плюс работа
против сил трения FTp AS. Но FTp = kmg cos а и AS = Al/cos а

216

рассмотреть все наклонные плоскости и сложить элементарные работы,
то общая работа будет равна
А = ^ ДЛ = mgC^ ДА + k 2 Al) = mgh + kmgl.
Работа определяется только высотой горы h и длиной I ее основания.
165. Сила, приложенная к рукоятке, будет минимальна, если
она составляет с ней прямой угол. Обозначая через F значение
искомой силы, на основании «золотого» правила механики будем
иметь 2nRF = Ph. Отсюда F — Ph/2nR.
166. По определению коэффициент полезного действия rj =
— Axl(Ai-\-A^, где А1 = РН—работа по поднятию груза Р на
высоту Я, а Аа — работа, совершаемая при этом против сил трения.
Так как сила трения способна удержать груз в равновесии, то работа
этой силы не может быть меньшей, чем работа Ах. Минимальное
значение работы сил трения A2 = AX. Следовательно, т) С 50%.
167. За время подъема человека по лестнице шар опустится на
некоторую высоту h. Следовательно, работа, совершенная человеком,
пойдет на увеличение потенциальной энергии человека на величину
m g ( l — h ) и на увеличение потенциальной энергии шара на величину
mgh (на шар без человека действует подъемная сила mg, направленная
вверх); отсюда
A = m g (l—h) + mgh=mgl.
Этот результат можно получить сразу, рассчитывая работу человека
в системе, связанной с лестницей.
Если человек поднимается со скоростью v относительно лестницы,
то относительно Земли он имеет скорость v—vu -где. —скорость
шара во время подъема человека. По закону сохранения количества
движения (v—v1)m =M v 1. Отсюда v-
168. Для того чтобы прогнать за единицу времени вдвое большее
количество воды, нужно сообщить вдвое большей массе воды вдвое
большую скорость. (Работа мотора идет на сообщение воде кинетической
энергии яю2/2.) Поэтому мощность мотора должна быть увеличена
в восемь раз.
169. 1) На подъем воды из ямы затрачивается работа
A ^ p g ^ S . ^ H = ^ p g S H \
где р—плотность воды. На сообщение воде кинетической энергии
затрачена работа
х 1 н о 2
г ~~2 Р ~2~
Скорость о, с которой вытекает вода из трубы на поверхность земли,
определяется из соотношения (Я/2) S = jtftVr. Полная работа равна

217

2) ‘Работа, затраченная на «ядвем веды <во «тором случае, меньше
-А) «а величину ДА ‘= pgSjft (®—Л/2). Работа, затраченная на
сообщение воде кинетической энергии, равна А% =-^1 — р (—ffS /2 -h S■i P■ .
Полная работа ^ ‘ = j4x— +
470. Проще всего решить задачу в системе координат, связанной
с эскалатором. Человек пройдет относительно него расстояние I =
= A/sin a — f от, еде trr—путь, пройденный эскалатором. При этом
он должен совершить работу А — (Л/sin a-(- vx) mg sin ce, так как во
время подъема сила /добыла приложена на пути / и составляла с ним
угол 90°—а. Часть работы mgh идет на увеличение потенциальной
энергии человека, другая часть работы, mgm sin a, вместе с работой
мотора, приводящего эскалатор в движение, идет на преодоление <
сил трения.
•171. Энергия пружины, оттянутой з а среднюю точку Q, равна
Wf—(2А)*2/2. Когда пружину отпустили, ее энергия стала равной
Wv— kx2/2, так лкак за время перераспределения у пру г, их деформаций/
в пружине масса m не успевает сдвинуться. Следовательно, потери
энергии в пружине Wt—Н^а= кх?/2. Это, конечно, грубая оценка.
172. Человек, действуя .с силой F на пружину, совершает работу
A f=— FL. Одновременно на пол вагона со стороны человека
действует сила трения Работа этой силы A2 = FL. Следовательно,
полная работа, совершенная человеком в системе координат, связанной
с Землей, равна нулю, так же как и в системе, связанной
с поездом.
173. В системе псезда совершенная работа равна потенциальной
энергии растянутой пружины Л*=’№/2, так как сила трения между
человеком и полом вагона в этой системе не совершает работы.
В системе, связанной с Землей, работа человека по растяжению пружины
равна- произведению средней силы Ы/2 на пройденный путь
L — I, т. е. Ax=(kl/2}(L—/). На пол вагона человек действует с той,
же средней силой kl/2. Ее работа A2 — (k42)L, Полная ,работа в данной
системе координат A — A1-{- Ai = kfif2 та же, что и в системе1
вагона.
474.1На основании законов сохранения количества движения и
энергии можно записать следующие уравнения:
mxvl -f m2y5 = + m2u’,
mjBf • щв| _ т хн’г
2 + 2 ~ 2 ^ 2 ’
где v’ и o ‘—скорости шаров после соударения. Решая данную систему
уравнений, получим
v, _ (т!—т.2) Vj + im ^ ^ (т2—т1)у2+ ^ Л
1 тгА-т2 * * тх-)-т2
1) Если второй шар до удара покоился (е2 = 0), то
n’==(mi—т^чхЦтхАгЩ), 2 т , %/(»%+яг*).
При « ! > т2 первый шар продолжает двигаться в том же направлении,
что и до удара, но с меньшей скоростью. Если т± < т2, то

218

первый шар отскакивает после удара назад. Второй шар будет’двигаться
в ту же сторону, в которую двигало* до удара первый шар.
2) Если яг1 = /п2, то
о’ = 2mv2/2m = v2, v’% = 2mv1/2m = vL.
Шары при ударе обмениваются скоростями.
175. Энергия упругой деформации, станет максимальной тогда,
когда относительная скорость шаров станет равной нулю. Для этого
момента времени закон сохранения механической энергии и закон
сохранения, количества движения можно записать следующим образом:
тр_
+ m2t>2 = («! + т,) и,
где и—абсолютная скорость шаров в тот момент, когда они обладают
максимальней- энергией- W упругой деформации; Следовательно,
wtiti? . m2o | (yn1t)1+ m 2o2)a__OT1m2(Pi— v2)2
2 2 2 (т + щ ) 2(m1+m 2y
176. В-результате упрушго соударения левый, брусок приобретает
скорость V. Правый брусок в этот момент временйещн покоится, •
так- как. пружина не деформирована; Обозначим, через. аг и щ скорости
левого и- правого брусков в произвольный момент времени,
а. через х —абсолютное удлинение пружины в тот же момент времени.
На основании законов сохранения количества движения и энергии
имеем
т («1+ и 2)=тс»,
mnf», т н | , Ы* то*
~2 *»1 г 2 2 »
или йх2= т [о2—(и|;+ «!).] • Заменяя в последнем уравнении v через
« i + “2> получим &х2= 2 т « 1н2. Следовательно, u1Ut = kx212m и
Ul-j-u2= o . Из двух последних выражений видно, что иь и и2 будут
иметь один и тот же знак—оба бруска движутся в одну сторону.
Величина х2 будет иметь максимальное, значение тогда, когда
произведение скоростей щ и и2 будет максимальным. Следовательно,
для ответа на второй вопрос, поставленный в задаче, нужно найти
максимальное значение произведения и1и2 при условии, что сумма
и,-г «2 постоянна и равна v. Рассмотрим очевидное неравенство
,(«1—и2)*~3* 0, или nf—2ujt(2-|-U2 0. Прибавим к правой и левой
частям неравенства Лиф?.. Тогда и\ + 2и1иг-\- и\ 5 = 4и1и2, или (их +
+ и2)2^ 4 и хи2. Так как ul -\-u2 = v, то 4uj«2< o 2. Следовательно,
наибольшее значение uLu2 равно О2/4, и оно достигается при u1=u2=v/2.
Расстояние между брусками в этот момент равно .
I ± хтз% =1 ±r v Т т/2к. ,
177. До тех- пор, пока нижняя, пластинка- лежит на столе, из
закона сохранения- механической энергии следует:
kx2 ky2 . ,. me2 ■*
-^2 —m g * :=-7£-\;mgy+~2-

219

где у т— удлинение пружины, v—скорость верхней пластинки. В момент
отрыва нижней пластинки от стола
ky = mg, y = mg/k,
причем v > 0. Учитывая эти соотношения, получаем из (1)
mv2 ■ kx2 3 m2g2
~ 2 ~ ~ 2 т^к ~~2~2§~ > ^
Для того чтобы выполнялось (2), должно быть х > 3mg/k.
Скорость vc центра масс в момент отрыва нижней пластинки от
стола равна vc — v/2. После отрыва нижней пластинки от стола центр
масс будет двигаться вверх равнозамедленно с ускорением g й начальной
скоростью Vc. Следовательно, максимальная высота подъема
центра масс равна
Н — ^2 g—~ 811g ‘ нH —8~g ({ m— — 22gеXх -3З ^k }) ’
где Я отсчитывается от положения центра масс в момент отрыва
нижней пластинки от стола.
(Разобранная задача дает представление о процессах, происходящих
при прыжках в -высоту.)
178. В системе отсчета, связанной со стенкой, скорость шарика
равна v-\-u. После удара в той же системе отсчета скорость шарика
будет —(ti + n). Скорость шарика после удара относительно неподвижной
системы отсчета равна
— (о + н) — « = ~ — (о + 2м).
Кинетическая энергия после удара от(о+2и)2/2. Кинетическая энергия
до удара ото2/2. Изменение кинетической энергии равно
2mu(uJr v).
Теперь подсчитаем работу упругих сил, действующих на шарик
при ударе. Пусть удар длится время т ; предполагаем для простоты,
что во время удара упругая сила постоянна (результат не
зависит от этого предположения). Так как в результате удара
количество движения изменилось на величину 2от (о+и), то упругая
сила равна F = 2m(o-f-u)/T. Работа этой силы
A =*FS = Fux = 2от (v+ и) ит/т = 2от (о-j- и) и.
Как легко видеть, эта работа равна изменению кинетической энергии.
179. 1) До момента, когда веревка натянется, камни падают свободно:
S ^ g P /2 , S2 = g ( t—т)2/2.
Момент натяжения веревки определяется из условия l = Sx—S2.
Отсюда / = Зс, = 44,1 м, S2 = 4,9m. Время отсчитывается с момента
падения первого камня. При натяжении веревки происходит
упругий удар, и камни обмениваются скоростями (см. задачу 174).
В момент удара vt = g t~ 29,4 м/с, o2= g ( l—т)=9,8м/с.
Время tx падения первого камня (после того как веревка натянется)
находится из условия
h -S i£= o it l -\-gtl/2.

220

Отсюда ti & 1,6 с, <2 « 1 ,8 с. Первый камень падает 4,6 с, второй
2,8 с. 2) В случае неупругой веревки скорости камней после ее натяжения
выравниваются (неупругий удар): v= (v1-{-v2)/2—19,6 м/с.
Время падения камней’ после того, как веревка натянется, определяется
уравнениями
Л—S i= v tl+ g t[ ‘/2, h—S2- v t ‘i -]-gt’21/2.
Si и S2 те же, что и в первом случае. Отсюда t[ я 1,2 с, я 3,3 с.
Первый камень падает 4,2 с, второй 4,3 с.
180. Если отклонить один правый шар, то после удара слева
отскочит крайний левый шар на угол, равный углу отклонения правого
шара. Если отклонить одновременно два шара и отпустить их,
то после удара слева отскочат два крайних левых шара. Если отклонить
три правых шара, отскочат три левых и т. д.
При ударе первого шара о второй первый шар остановится,
передав свое количество движения второму шару (см. решение задачи
174); второй передаст это же количество движения третьему,
третий — четвертому и т. д. У крайнего левого шара нет «соседа»
слева, поэтому шар отскочит (если нет трения и потерь энергии) на
тот же угол, на который был отклонен крайний правый шар. Когда
левый шар, после отклонения на максимальный угол, ударит предпоследний
шар, процесс передачи количества движения по цепочке
шаров повторится в обратном направлении.
При отклонении одновременно двух правых шаров они передадут
свое количество движения цепочке не одновременно, а по очереди,
через очень малый (неуловимый на взгляд) промежуток времени.
Таким образом, цепочка шаров получит не один «двойной»
импульс, а два* которые будут распространяться по цепочке с некоторым
временным интервалом. Крайний левый шар отскочит, получив
«первую порцию» количества движения. Следом за ним отклонится
его «сосед», получив следующую порцию количества движения,
переданную ему от крайнего правого шара.
При отклонении трех правых шаров цепочка получит три следующих
один за другим через очень малые промежутки времени
порции количества движения соответственно от третьего, второго и
первого шаров. Если отклонить и одновременно отпустить четыре
шара, то отскочат слева также четыре шара, а два останутся неподвижными.
181. Ударяющий шарик отскочит назад, следующие шарики до
стального останутся неподвижными. Стальной шарик и все последующие
начнут двигаться влево, причем скорости их будут различны.
Наиболее быстро будет двигаться крайний левый шарик. Следующий
будет двигаться медленнее и т. д. Шарики разойдутся (см. решение
задач 174 и 180).
182. Пусть груз 2т опустился на высоту Я. Тогда грузы т поднимутся
на высоту ft (рис. 347). На основании закона сохранения
энергии
2m g h — \- ^ Y ^ — \^ ^ -= 2m gH , или v l+ v l = 2g(H—Л),

221

где i»!—скорость грузов » v a %—скорость груза массы 2т. <Яа
мере опускания груза 2т, его скорость v2 приближается к скорости
vlt так как углы между участками
нити, ..перекинутыми ■ через блоки,-
стремятся к нулю. В пределе v2 « о,.
.Одновременно Н—Л и I. Следовательно,
предельное значение скорости
грузов равно 0== y»g/.
183. пути, пройденные ими за равные
малые промежутки времени, одинаковы.
Эти пути одинаковы при таком
значении угла AN В, при котором
опускание груза тг на As=^N’K (рис.
348) будет сопровождаться’ увеличением
длины-участка нити AN В также
на величину As. Поэтому при равенстве
скоростей # /С = ЯК—£W=As)2
и FK = AK — AN = As/2. Треугольники
NHK и NFK тем ближе к прямоугольным, чем меньше мы
выберем отрезок As. При As-»-0 углы NHK и NFK стремятся к

222

прямым, а углы KNH и K.NF—тс 30°.: Следовательно,- скорости будут
равны при £_ ANB = \2(f. Используя закон сохранения энергии,
найдем значения этих скоростей:
Отсюда
migh = 2 (2— V 3) migh-Jr r^ p ^ о*.
v2« ~ 2ne h«. —я*1———2~ (Л2—— » 0. „ га!-)-я2
Грузы будут совершать колебания около положения равновесия,
которому соответствует значение угла j4A’fl = 2arccos(OT1/2m2) « 149°.
Углу AN В = 120° соответствует максимальное отклонение от положения
равновесия.
184. Так как проскальзывание доски по каткам и катков погоризонтальней
поверхности отсутствует, то расстояние между осями
катков во время движения останется постоянным. Поэтому движение

223

диски: будет поступательным. Доска будет перемещаться ,в гЪриаон-
га«>ном направлении и одновременно двигаться вниа вдоль, катков.
Если- катки -сместятся на некоторое расстояние I, то каждая точка
доскн(в частности, ее центр тяжести А) пройдет вдоль горизонтали
то: же-расстояние I n одновременно переместится на это же рас-
стояние вдоль-катков: АВ = ВС = I (рис. 349). (Последнее становится
особенно. очевидным, если рассмотреть движение катков в системе
координат, перемещающейся вместе с катками.) В результате центр
. тяжести Доски будет двигаться: вдоль прямой АС, наклоненной к
горизонту под углом а/2, так как треугольник ЛВС равнобедренный.

Движение будет* равноускоренным. Доска приобретет кинетическую
энергию за счет уменьшения потенциальной: mv2/2 — mgl sin а, или
» *= 2g /s in a . С другой стороны-,- при равноускоренном движении
о*= 2 ctS, где S = АС=21 cos (а/2). Следовательно, ускорение а —
= v2/2S= g sin (а/2).
185. Подсчитаем разность потенциальных энергий для двух положений
цепочки: цепочка полностью лежит на доске и часть цепочки
длияы.х.свешивается с диски. Эта разность равна силе тяжести
(Mftljxg свешивающейся части, умноженной на х/2, поскольку
цепочка однородна и Центр тяжести свешивающегося конца находится
на расстоянии х/2 от края доеки. На основании закона сохранения
энергии имеем Mv2/2 — (Mg/41) х2, или о = У gx2/21. Ускорение
в этот же момент времени можно найти из второго
закона Ньютона: Ma=(-M/2/)gr*Следовательно,
a—gx/21. Для. подсчета реакции края доски найдем.
первоначально натяжение цепочки в точке
соприкосновения с-доской.. Оно равно произведению
массы части цепочки, лежащей на доске, на
ускорение цепочки: Mxg(2t—x)/Al2.
Рассмотрим теперь очень малый элемент це- Рйс. 350.
почки, соприкасающийся с краем- доски. На этот
малий элемент цепочки действуют три силы. (рис. 350). Они вызывают
изменение его количества движения по- горизонтали и вертикали:
(N cos а — F)At = — Mv2 At/21, .
(F ^ -N sin a) At.= Mv2 At/21,

224

Следовательно* угол наклона силы N к горизонту а = 45° и У »
= Mgx (/—х) V 2//2.
186. Обозначим через v скорость тележки. Горизонтальная составляющая
скорости маятника относительно тележки равна и cos Р
(рис. 351), а относительно рельсов равна о + и cos р. В горизонтальном
направлении на систему внешние силы не действуют. Поэтому
на основании закона сохранения количества движения имеем
m(v-\-u cos PJ+iWo = 0, (1)
так как вначале система покоилась. Вертикальная составляющая скорости
маятника относительно тележки и рельсов равна и sin р. На
основании теоремы Пифагора квадрат скорости маятника относительно
рельсов равен (o-J-и cos P)2-f-“ 2 sin2 р. Используя закон сохранения
энергии, получаем второе уравнение, связывающее скорости
о и и:
~ | (и cos р + о )2+ м 2 sin2 pj -|- ^ — v 2 = tngl (cos Р —cos а). (2)
Из уравнений (1) и (2) можно найти
2 _ 2m2gl (cos р — cos «) cos2 р
0 ~~(М + m) (M + /n sin2 р)
В частном случае при р = 0 (считая т/М 1) получаем
о2 = 2 | 2 ^ ( 1 — с о з а ),
или
— 2 | s i n
187. Обозначим через v скорость клина, а через их и иу — горизонтальную
и вертикальную составляющие скорости и бруска относительно
неподвижной системы отсчета (рис. 352). На основании
законов сохранения количества движения и энергии можно написать:
— Mv-\-mux = О,
Мо2 т , 2 , 2ч ‘
~ 2 ~ + Y (ux + uy) = meh-
Заметим, что угол се с горизонтальной плоскостью составляет не
абсолютная Скорость бруска и (под абсолютной скоростью в данно

225

случае поймаем скорость относительно неподвижной горизонтальной
плоскости), а относительная скорость иотн, т. е. скорость бруска
относительно движущегося клина.

188. Скорость стержня относительно движущегося клина направлена
под углом а к горизонту. Если к этой относительной скорости
прибавить скорость клина, то в результате получим абсолютную
скорость стержня и (рис. 354). Очевидно, что отношение скоростей
равно и/и= tg а.

226

Исключая из этих двух уравнений я, получим выражение для «
о— y~2mgA/(Af-f m tg s а). Тогда для относительной скорости стержня
мы можем написать
и отн = ^п1о Q, лу / I 2mgk
Скорость стержня

Йз последнего выражения видно, что скорость стержня меняется
с ^.пройденным путем h по закону равноускоренного движения:
и — Y-2ah. Следовательно, ускорение стержня а= M t ^ a , ‘

227 СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ. Работа и энергия. Ответы.

Работа и энергия