ЗАДАЧНИК Кванта

ЗАДАЧИ

Страница переведена на новый сайт https://myeducation.su/ : страница

ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЖУРНАЛ Квант (6 июнь 1972)

Решения задач можно посылать не позднее чем через полтора
месяца после выхода из печати соответствующего номера журнала
по адресу: 117071, Москва В-71, Ленинский проспект, 15. изда-
тельство «Наука» , редакция журнала «Квант» . После адреса на
конверте укажите, решения каких задач вы посылаете; например:
«Задачник «Кванта», М146, М148». В начале письма укажите
свою фамилию, имя, отчество, домашний адрес, а также класс
и школу, в которой вы учитесь.

М146.а) В вершинах правильного
7-угольника расставлены черные и
белые фишки. Докажите, что най-
дутся три фишки одного цвета, ле-
жащие в вершинах равнобедренного
треугольника.
б) Верно ли аналогичное утверж-
дение для 8-угольника?
в) * Выясните, для каких пра-
вильных л-угольников аналогичное
утверждение верно, а для каких —
нет.
А. Романов
М147. Докажите, что если че-
тырехугольник A BCD, вписанный в
окружность, таков, что касательные
к окружности в точках А и С пере-
секаются на продолжении диагонали
BD, то
а) касательные в точках В и D
пересекаются на продолжении диаго-
нали АС;
б) биссектрисы внутренних уг-
лов А и С четырехугольника пере-
секаются на диагонали BD (а углов
В и D — на АС).
И. Ф. Шарыгин
М148. Последовательность дг0, xlt
х.,,. . . определяется следующими ус-
ловиями: А’о = 1, *! = X, для лю-
бого п > 1 (а -г- рТ*„ = апх„х0 +
+ • . • + f>nxoxn. Здесь к, ‘а, р —
заданные положительные числа. Най-
дите хп и выясните, при каком п ве-
личина хп будет наибольшей.
А. Л. Лопшиц
36
М149. Пусть 0 — точка пере-
сечения диагоналей четырехуголь-
ника ABCD. Докажите, что
а) если равны периметры тре-
угольников ABC, BCD, CD А и DAB,
то ABCD — прямоугольник;
б) если равны периметры тре-
угольников А ВО, ВСО, CD0 и DA0,
то ABCD — ромб.
Н. Б. Васильев
М150*. Из чисел 1, 2,. . ., k сос-
тавляются всевозможные наборы (а,,
а.г,. . ., а„) длины п {легко видеть,
что их к’1). Выбраны два подмножест-
ва Р и Q таких наборов (один и тот же
набор может входить и в Я, и в Q).
Известно, что если взять произволь-
ный набор {ру, p.lt. . ., р„) из Р и про-
извольный набор (<7м <7>,. — -, q,,) из
Q, то они будут совпадать хотя бы
в одном месте (то есть р4- = q{ для
некоторого j). Тогда либо в Р, либо
в Q не более чем kn~x наборов.
Докажите это утверждение
а) для k — 2 и любого п;
б) для и = 1, 2, 3 и любого k ^ 2;
в) для произвольных й^2ип^
> 1-
Попробуйте найти другие огра-
ничения на количество элементов
в подмножествах Р и Q, Связанных
таким условием.
В. Б. Алексеев
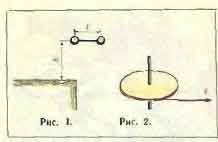
Ф158. Гантелька, расположенная
горизонтально, падает с высоты h
и ударяется одним из концов о стол

36 ЗАДАЧНИК Кванта 

(рнс. 1). Какое расстояние пролетит
гантелька после удара до того, как
она опять станет горизонтальной?
Гантелька состоит из двух одинако-
вых тяжелых шариков, насаженных
на невесомый стержень длины /. Удар
гантельки о стол абсолютно упруг.
Стол после удара мгновенно убирают.
Олимпиада МФТИ, 1971 г.
Ф159. Разность между давлениями
внутри и снаружи резинового шарика
возросла на ctj%, а при этом радиус
увеличился на qx%. На сколько
процентов возрастет радиус шарика,
если разность между давлениями внут-
ри и снаружи шарика возрастет на
И. Ф. Гинзбург
Ф160. Диск радиуса R раскру-
чивают вокруг вертикальной оси с
помощью веревки длины I, которую

тянут с постоянной силой F (рис. 2).
¦После этого диск соскакивает с оси
и попадает на горизонтальную плос-
кость. Сколько оборотов сделает
диск на плоскости до полной оста-
новки, если его масса равна т, а ко-
эффициент трения диска о плоскость
равен /г?
С. А. Беляев
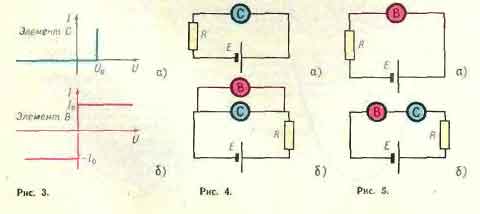
Ф161. Вольтамперные характе-
ристики элементов С и В показаны
на рисунках 3, а и б (это идеализи-
рованные вольтамперные характе-
ристики стабилотрона и баретора).
Какой ток идет через элемент С в це-
ня х, показанных на рисунке 4? Ка-
ково падение напряжения на эле-
менте В в схемах, показанных на
рисунке 5?
А. Р. Зильберман
Ф162.. Противостоянием Марса на-
зывается момент, когда Марс, Солн-
це н Земля находятся на одной пря-
мой. Великое противостояние — это
момент, когда расстояние Земля —
Марс минимально. Считая, что орбита
Земли — круг, а орбита Марса —
эллипс, найти, через сколько лет
повторяются великие противостоя-
ния.
Полный оборот вокруг Солниа
Марс делает за 687 дней.

37 ЗАДАЧНИК Кванта 

РЕШЕНИЯ
В этом номере мы публикуем решения задач М106—М107
Докажите, что если для чисел р,.
(<7i — QtY2 + i
го квадратные трехчлены
М106
. <?t. q2 выполнено иераьеиспю
— Р2ЧР1Я2 — P2QO < 0.
X2 -г р,Л» — </,, V- -г />гЛ -t» (?2
имеют вещественные корни и между двумя корнями каждого из них лежит корень другого.
Нам понадобятся следующие свойства квадратного трехчлена:
/(а) х- + рх + </¦
1. Если для кякого-то числа с выполняется неравенство f(c) < 0. то уравнение Цх) -О
имеет дпа различных действительных корпя.
2. Если для чисел с и d выполняется нераоеиство /(с) /(^ < 0, то уравнение /(ж! -0
имеет дна действительных корня, причем одно из чисел с и d лежит между этими корнями,
а другое — мет.
Эти свойства очсешдны, если посмотреть на график (рис. I). но мы все-таки докажем
их строго.
П ‘ 2 1
1. Поскольку f{c) = с1-\-рс-\-q ^ |c -\-~y\ — ~{Р’ — 4</)<0. то рг-Ац >0
и уравнение /(л) -0 имеет два корпя ~о~( — р ± 1/р4 — 4<? )¦
2. Поскольку / (с) f (d) < 0, то/ (f) или [ (d) огрицптелыю. По свойству (I) уравнение
f (х) л\кч-т л па корни. ОСюзначим их а и р\ Тогда /(л) — л- + рх Ц- ц • ¦¦¦ {х —a)(.v — |^).
Число х лежит между корнями тогда и только тогда, когда (а- — а){х — fty < 0 или / (л) < 0.
Поскольку одно из чисел / (с). / (d) or-
рииателыю, а другое положительно, ю
ровно одно и:* чисел cud лежит между
корнями.
Перейдем теперь непосредственно к
решению ладачн. Введем обозначения:
;\ (л) л-+/>,*» + <?,.
j., (л) — л- +
/? Gi — c/J15 -f- (/)i—
Мы Должны доказать, чю если А? < 0. то
каждое ил уравнен mi /, (х) — 0 и /г (.vj :
0 имеет 1Ю дна различных дспстоитель-
иых корпя н между корнями одного из
inix ypamicii 11Г1 лежит ровно один корень
другого.

Рассмотрим разность
Заметим, чго р, — />«, ^ 0, так квк тот pt — р* 0, то /? -¦ — (</, — <?г(- 2s 0, ччи
причем, конечно, /:, (л-) можно записать так:
/Ч jl
проТШЮрСЧИТ УСЛОВИЮ. ПОЭТОМУ VPiinilCllllC /-, (V) О ИМСС1 КОГЮНЬ V «~ —~ ~i
Р[ — Г2
Кроме того, как следует n:i (]).
7i(T)—=/a(T>-
C)
Теперь квадратный трехчлен /2 (.v) (умноженный на коэффициент (ру—р«)а «разде-
лим с остатком» на /., (л), го есть напишем тождество
(Pi — Ра)» /2
.гз <-*) 4 (л) +
Мы не случайно нсполмопллм ту же букву R: остаток ранен именно выражению /?. дан-
ному п условии задачи. ДсПслшголыю,
(Pi —
(Pi ~ Ра)»
Подстянпп у it (I), получим (учитывай, что (я (yj 0):
(Pi -PaK /*(V) ¦ Л <0- (о)
Поэтому /, (у) — /2 (у) < 0. Следовательно (ко егчжегку (Ij) оЛй уравнения имеют но Д1 а
действительных корня. Обозначим нх соответственно a,, |i, н а», fi2. Тогда
Мх>«(х-а2)(*-Рг)- F)
Теперь, используя [юследоклтелыю (I), B), F) и EJ, получаем.
Л (*г) Л (PJ /a («J /a (Ps) «¦¦=
: (Pi — /J2)’: («з — VHP» — V> -MP, — P2V- /j (V) /? < 0, G)
откуда следует (но свойству {‘2\), что корни уранненнй чередуются.
Используя графики, результат надачи и основное в нашем решении соотношение (i»|
можно объяснить в два слова (рис. 2). Алгебраическая подоплека нашего решения более
глубока.
Из нашего решения, да u in рисунка 2 видно, что R -= 0 тогда и только тогда, косой
квадратные трехчлены /t и /а имеют общий корень (или совпадают). Эго обе го я тел ьег во
можно использовать в задачах такого
типа: каким условиям должны удовле-
творять числа /. н и, чтобы ураннення
хг + ах- — I = 0 и х- + fix- — Ал- +¦ ц ¦—¦ 0
имели общин корень? Достаточно под-
ставить п выражение R значения р, ¦— А,
Я] ~ —1. Рг ~ !1 —Л- tfs » !’¦ » нуж-
ное условие готово:
Qi + t)= + Bа — }i) (ц — а + иХ) = 0.
Оказывается, что и для двух мно-
гочленов произвольной степени
/t (дг) г= о,л:л + Ь,д:п-» + … + с,.
можно выписать такой многочлен R от
я,, о2, frj, Ь.г с,, <«s, чго условие
У? =— Обуяет выполняться тогда и только
тогда, когда /, и/а имеют общий дели-
тель (многочлен от х степени 1 или вы-
ше). R называется результантом много-
членов /, и /о.
Рис. 2. Для того чтобы корни квадратных
трехчленов I и f.> были действительны и пе-
ремежались, необходимо и достаточно, что-
бы точна пересечения их графиков лежала
ниже оси абсцисс, то есть чтобы число
/i (V) — h (V) —
было отрицательным.
/ГТ
В курсе высшей алгебры приводится компактная запись результанта п виде «опреде-
лителя», составленного из коэффициентов /, и /2.
Особенно прозрачным становится понятие результанта, когда /, и /s разлагаются на
линейные множители:
а, (х
(а —
/2 =¦ о2 (дг — а3)(х —
(д: —

38 ЗАДАЧНИК Кванта Решения 

(на множестве комплексных чисел это всегда так, ведь там любой многочлен имеет корень).
Тогда, как можно доказать,
= R
h)=aim^n («i -a*W, -аг) . . . fr, —
где произведение берется по всем парам корней /г и /2 (то есть в нем тп сомножителей).
Проверьте, что в кашей задаче R = (ах — аа)ф, — aa)(at — рг)(аа — р»г), и подумайте,
как с помощью этого выражения R через корни (быть может, комплексные!) квадратных

трехчленов решить задачу другим спосо-
бом. Из равенства (8) вытекает такое,
уже встречавшееся нам в частном случае,
равенство:

Осиовнос свойство результанта с уче-
том комплексных корней можно сфор-
мулировать так: R 0 пюгда и только
тогда, когда jv и /2 имеют общий корень.

MI07
а) Дан выпуклый многоугольник
AtA2 . . Л« (рис. 3). На стороне i4,/4,
взяты точки J3, и ?),, us стороне АгАя —
точкм В.. и D3, … на стороне Л«Л! точ-
ки Вп и ^! тлк, что если построить нв-
ряллелограммы Л,В,С,?), ^gfijCjDg….
. . . , AnBnCnDn, то прямые Л,С|.
i4,C’j ЛлСп пересекутся в одной
точке. Докажите, что
f>) Докажите, что для у
верно и обратное утверждение: пусть из
стороне -4 (.-1 а выбраны точки й, н D,. «а
стороне .4 341 — точки /?s к Оя, яа стороне
/4 л.4, — точки йя » Oi TaK- чго
тигля, гелн построить параллологрвммм
у» i/J1fT,?>1. MtfisCgJE),, ^aOaCaOs. то пря-
мые .-^С,. Н»Са н ЛдС, пересекутся в
одной точке.
а) П\ст1> О — точка пересечения. За-
пишем равенство, которое нам нужно
доказать, так (сдвинем в знаменателе нее
сомножители, перенесем AlDl в конец):
ASD2-A:1D3- . . . ¦A:,Dn-Al[)l -l»
Теперь Заметим, что отношения отрезков
,1,/J, Л., В., АпВп
П—Г»» В А > • ¦ • » П Л соответствен-
но равны отношениям площадей тре-
угольников (площадь треугольника Л1Л’/-
х:ы обозначим тлк: S (MXL))

Но последнее равенство очевидно. Действительно, площади трсуголышкоп AiBfi и AiDfi
для каждого i 1,2 п равны, поскольку они имеют общую сторону Аг0 и равные
высоты (рис. 4); высоты, опущенные из вершин В{ л Di на сторону А-,0, равны, потому что
диагональ AjCj делит параллелограмм Л,-/^С,-?); i а два равных треугольника.
б) Ortpacuyto теорему можно вывести \\л прямой. Пусть Р — точка пересечения пря-
мых AiCt и АЯС2. Предположим, чю прямая А3Р не проходит через точку С3. Тогда оня
пересекает одну из cropufi B-dC3 или D3C{ параллелограмма AnB3D3C:t, скажем, D3C3
(рис. 5) it точке С’3. Выберем на стороне .4Э.’1, такую точку В’3. что АЯВ’ЯС’ЯОЯ — парал-
лелограмм. Тонер it, согласно прямой теореме. А1В1-А2В2-АЯВ’3 AiDl-A2bs’A3Ds, с
другой стороны, но условию AlBi-AiB,.A3B3 — AlDl-AiD2-A3D3. поэтому Л35’й~
A3ft:t. следовательно, наше предположение о том, что точки С3 и С3 (и, следоьатель-
но. точки В3 и В’3) не совпадают, неверно.
В. JI. Гупкнмяхер

41 ЗАДАЧНИК Кванта Решения

 

ЗАДАЧНИК Кванта