Вычисление объемов с помощью принципа Кавальери
В. Л. Рабинович
Если хотите быстро ознакомится с содержанием статей, смотрите ниже.
Текст, для быстрого ознакомления (в тексте для быстрого ознакомления формулы могут отображаться не корректно):
Страница переведена на новый сайт https://myeducation.su/ : страница
ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЖУРНАЛ Квант (6 июнь 1972)
Что такое объем? Как вычислить
объем конкретного тела? Уже для
ответа на первый из этих вопросов
даже для такого «простого» случая,
как прямоугольный параллелепипед,
хотя бы одно из измерений которого
не соизмеримо с фиксированной еди-
ницей длины, приходится пользовать-
ся рассуждением, связанным в той
или иной форме с переходом к пре-
делу бесконечной последовательности.
При переходе к более сложным во-
просам — об определении и вычис-
лении объема произвольного парал-
лелепипеда, затем произвольной приз-
мы, потом (очень важный шаг!) пи-
рамиды, наконец, «круглых» тел: ци-
линдров, шара и шаровых сегментов
— приходится использовать все но-
вые и новые переходы к пределам,
буквально нагромождая их друг на
друга.
Рассуждения эти, с одной стороны,
таят немало тонкостей и трудностей,
с другой — представляются (внешне)
довольно-таки «стандартными». И не-
посильность учета всех этих тонкос-
тей и оговорок в школьном курсе
математики, и обманчивая «похо-
жесть» всех этих рассуждений о пре-
делах в равной степени приводят к
тому, что на них (на рассуждения)
начинают смотреть зачастую как на
неизбежные ритуальные заклинания,
не вдумываясь и не пытаясь постичь
их подлинный смысл и цель. Просто
пропускать их — тоже как-то «не-
удобно», «неприлично»: все-таки ма-
тематика! . . .
Так нельзя ли хотя бы до лучших
времен одним махом разделаться со
всеми этими неприятными разгово-
рами о пределах? Оказывается, очень
—
даже можно. Для этого достаточно
принять в качестве постулата
(аксиомы) так называемый принцип
Кавальери *). Именно принять,
а не доказывать. Это, конечно, не
означает, что принцип этот вообще
нельзя доказывать и обосновывать.
Больше того, рассуждения о «неде-
лимых», с помощью которых сам
Кавальери пришел к его формули-
ровке (во многом, кстати, порази-
тельно предвосхищенные еще Архи-
медом с его «методом исчерпывания»),
были уже довольно близки к методам
интегрального исчисления Ньютона
и Лейбница, посредством которых
в наше время и определяются объемы
«со всей строгостью». Но раз уж на-
шей целью как раз и было н а
этом этапе избавиться от вся-
ческих пределов, неделимых, бес-
конечно малых и т. п., то разумнее и
честнее будет не пользоваться ни-
какими суррогатами. В конце концов,
мы же знаем, что геометрия строится
на базе аксиом. Так вот — будет
еще одна аксиома. (По ходу дела
мы увидим, что фактически придется
воспользоваться еще парой аксиом,
которые, впрочем, можно восприни-
мать и как определения.)
Итак, формулируем принцип Ка-
вальери:
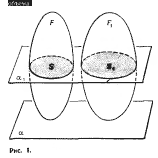
Если при пересечении двух тел **)
F и Ft (см. рис. 1) плоскостями,
параллельными одной и той же плос-
кости а, в сечении всегда получаются
фигуры, площади которых находятся
*) Бонавеитура Кавальери A598—
1647) — итальянский математик, ученик Га-
лилея.
**) Под «телом» мы всюду понимаем
«нечто имеющее объем», не пытаясь точнее
определить заключенные в кавычках слова.
9 Вычисление объемов, принцип Кавальери.
6 постоянном отношении к(Х >• 0):
5 = XSa,
то объемы этих тел находятся в
том же отноигении:
V(F) = Mf i) •)¦
Счово «объем» здесь впер-
вые появляется не в «наводящих»
рассуждениях, а в составе строго фор-
мулируемого предложения; поэтому
нашу аксиому мы можем понимать и
как определение объ-
ема — конечно, лишь для таких
тел F, что для них найдутся соответ-
ствующие Fly для которых поня-
тие объема уже опре-
делено предварительно
(см. ниже).
Применим теперь принцип Ка-
вальери для вывода формул объемов
некоторых тел. Предварительно нам,
однако, придется напомнить, что объ-
ем куба, ребро’ которого равно еди-
нице длины, принимается
равным единице (такой куб
называется единичным**).
•) Обычно в литературе принципом Ка-
вальерк называют предложение, являющееся
частным случаем приведенного, когда отно-
шение площадей сечеиий. о котором говорит-
ся в предложении, равно единице. Однако у
самого Кавальери принцип приводится и ис-
пользуется и в указанной более общей форме.
**) Это первое из упомянутых выше допол-
нительных условий, которое можно понимать
или как аксиому об объеме единичного
куба, или как определение этого
объема.
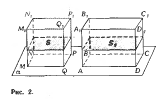
а) Произвольные призма и цилиндр.
Сначала рассмотрим прямоугольный
параллелепипед с изменениями, рав-
ными 1, 1 и A (А может быть как ра-
циональным, так и иррациональным
числом). Пусть (рис. 2) в параллеле-
пипеде АСг АВ =— AAl = \,AD = А.
Рассмотрим» единичный куб MPlt ос-
нование которого расположено на
той же плоскости а, на которой на-
ходится основание ABCD паралле-
лепипеда. Легко видеть, что площади
сечений S, и S параллелепипеда и
куба любой плоскостью, параллель-
ной плоскости а, находятся в посто-
янном отношении h, то есть 5,=
= h-S. Спедовательно, по прин-
ципу Кавальери
V{ACX) = h-V(MP,)= h-\ = А*).
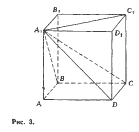
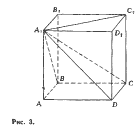
Пусть теперь дана произвольная
призма (или цилиндр) F (рис. 3)
с площадью основания S и высотой h.
Расположим параллелепипед ЛСД с
измерениями 1, 1, А так, чтобы его
грань ABBtA^AB — 1,АА} = 1)
находилась в той же плоскости а,
что и основание данной призмы F.
Поскольку AD = А, то и верхние
основания данной призмы и парал-
лелепипеда ACi лежат в одной плос-
кости. Тогда в сечении призмы F
любой плоскостью, параллельной а
и пересекающей призму, получится
фигура, равная основанию призмы.
Площадь этой фигуры поэтому равна
S. Та же плоскость в сечении с
*) Если принять в. качестве постулата
упомянутый выше частный случай принципа
Кавальери при ‘к = 1, то вместо только что
приведенной «аксиомы единичного куба» (см.
предыдущее примечание) придется взять это
соотношение в качестве «аксиомы прямоуголь-
ного параллелепипеда».
10 Вычисление объемов, принцип Кавальери.
параллелепипедом дает квадрат пло-
щади 1.
Условия принципа Кавальери вы-
полнены. Значит,
С,
V(F) —
Но мы нашли, что У(АС{) = Л.
Итак,
V(F) = Sh.
б) Произвольные пирамида и ко-
нус. Сначала рассмотрим частный слу-
чай. Куб ЛС, с ребром, равным h
(рис. 4), может быть расчленен на
три четырехугольные пирамиды
AXABCD, AlBCClBl и A^CC^D^
Эти пирамиды равны между собой.
Действительно, первые две пирамиды
могут быть совмещены так, чтобы их
основания (равные квадраты A BCD
и BiC^B) и равные ребра ААУ
и В1А1 совпали. Тогда и пирамиды
совместятся. Аналогично показыва-
ется равенство последних двух пи-
рамид *). Значит, объем каждой из
пирамид втрое меньше объема куба
АС
V{AlABCD) =-\-h3**).
Пусть теперь дана произвольная
пирамида F (или конус) с площадью
*) Необходимые совмещения любой нары
из этих трех пирамид могут быть реализова-
ны, например, при сращении одной из пира-
мид около оси AtC на угол 120*.
•*) Здесь мы используем последнее из
дополнительных определений (аксиом): объем
совокупности нескольких тел (в данном слу-
чае куба) равен сумме объемов этих тел (пи-
рамид). Равенство же объемов равных тел (пи-
рамид) легко следует из принципа Кавальери.
основания 5 и высотой Л. Располо-
жим эту пирамиду так, чтобы ее ос-
нование находилось в той же плос-
кости а, в которой находится осно-
вание рассмотренной только что че-
тырехугольной пирамиды AlABCD
{ее будем обозначать для краткости
Z7,). Можно считать, что вершины
этих пирамид находятся по одну
сторону от плоскости а. Тогда, ис-
пользуя теорему о сечении пирамиды
плоскостью, параллельной основанию,
легко получить, что площади сече-
ний обоих тел плоскостью, парал-
лельной плоскости а, будут отно-
ситься как площади их оснований.
Поэтому может быть применен прин-
цип Кавальери:
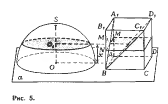
в) Шар, шаровой сегмент. Рас-
смотрим полу-шар с центром в О
и радиусом R. Продолжим плоскость
а ограничивающего этот полушар
большого круга и поместим на эту
плоскость основанием куб с ребрами,
равными R (рис. 5). Если мы отде-
лим от этого куба четырехугольную
пирамиду B/I^jCjDl имеющую
вершиной вершину В куба, а осно-
ванием — верхнее основание послед-
него, то получим некоторое тело, ко-
торое будем обозначать через /\.
Пересечем оба тела некоторой плос-
костью а’, параллельной плоскости а
11 Вычисление объемов, принцип Кавальери.
и отстоящей от а на расстояние х
(х < R). В сечении с пол у шаром эта
плоскость дает круг, площадь кото-
рого равна (R2 — хг)п. В сечении
же тела Ft той же плоскостью полу-
чится фигура, площадь которой равна
Rz — х2 (ибо M^N = NB ¦¦= х). От-
сюда ясно, что условия принципа
Кавальери выполнены. Следователь-
но:
Объем шара вдвое больше.
Найдем теперь объем шарового
сегмента F’ с высотой SO^ = h (см.
тот же рис. 5). Заметим, что приве-
денное выше для полушара рас-
суждение, показывает, что к сегменту
F’ и телу F\, полученному после
изъятия из прямоугольного парал-
лелепипеда МСу усеченной пирамиды
МгС1г также применим принцип Ка-
вальери. Поэтому (учитывая, что
BV — MXN = R — h)\
V(F’)-nV{F\)
откуда
» шар. ссгм. == ‘
-fA)
г) Тор. Тором, как известно, на-
зывается тело, полученное враще-
нием круга около оси, расположен-
ной в плоскости круга и не пересе-
кающей последнего. {Форму тора
имеет, например, надутая камера
автомобильной шины; в просторечии
тор часто именуют «баранкой».)
Для вывода формулы объема тора
представим себе, что тор F «лежит»
на плоскости а, касаясь ее по
некоторой окружности. Обозначим ра-
диус круга, при вращении которого
получен тор, через R, а радиус окруж-
ности, которую описывает центр кру-
га 0lt через а. Представим себе, что
на плоскости а «лежит» цилиндр F’
радиуса R и высоты а, касающийся
плоскости а по образующей SVS2.
На рисунке 6 оба тела изображены в
прямоугольной проекции на плос-
кость, параллельную оси вращения
тора. При этом цилиндр расположен
так, что его образующая не парал-
лельна плоскости проекции (ху —
ось вращения тора). Пересечем оба
тела плоскостью, параллельной плос-
кости а и отстоящей от О! на расстоя-
ние г (№г — SSi = R, 00t =
— AD = ВС = SXS2= а; см. рис. 6).
Эта плоскость в сечении с тором дает
кольцо, площадь которого равна, как
нетрудно подсчитать, 4ля (/» R* — г2 .
В сечении же цилиндра получится пря-
моугольник площади 2а V R2 — r2 .
По принципу Кавальери
V(F) -= 2mV(F1) = 2n2aR *.
д) Теперь мы легко выходим за
пределы так называемой «элемен-
тарной геометрии»; рассмотрим, на-
пример, сегмент параболоида вра-
щения. Парабола у = kx2 вращается
около оси Оу (см. рис. 7), образуя
некоторую поверхность вращения. Оп-
ределим объем тела F, ограниченного
12 Вычисление объемов, принцип Кавальери.
этой поверхностью и плоскостью, пер-
пендикуляром оси Оу и отсекающей
на этой оси отрезок ОК. ¦- Л (та-
кую форму имеет, например, авто-
мобильная фара). Будем считать дан-
ным также радиус основания сег-
мента KZ = а.
Рассмотрим прямую треугольную
призму FL высоты 1, в основании
которой лежит прямоугольный тре-
угольник с катетами, равными Л. Рас-
положим эту призму так, чтобы одна
из меньших боковых граней оказа-
лась лежащей в одной плоскости с
основанием сегмента так, как пока-
зано на рисунке 7. Тогда нетрудно
доказать, что в сечении сегмента плос-
костью, параллельной основанию, по-
лучится круг площади их2 -— я -4-;
та же плоскость в сечении с призмой
дает прямоугольник площади у-\.
Применив принцип Кавальерн, полу-
чим:
е) Применим, наконец, принцип
Кавальерн для вывода полезной в
приложениях формулы, связываю-
щей площадь плоской фигуры с пло-
щадью прямоугольной проекции этой
фигуры:
¦^проекции ~= «Фигуры’COS ОС,
где через а обозначен угол между
плоскостями фигуры и ее проекции.
Пусть фигура ADBC имеет своей
прямоугольной проекцией на неко-
торую плоскость фигуру AxDxByC^
(см. рис. 8). Прямые, проектирующие
точки контура фигуры ADBC (AAL,
ВВи СС1 и т.д.), являются образу-
ющими некоторой цилиндрической по-
верхности. Отложим на образующих
отрезки равной длины АА2 и АХАО
и проведем через точки А2 и Ап
плоскости,параллельные соответствен-
но плоскостям ABC и А^ВХСХ. Мы
получим два цилиндра — наклонный
(АВ3) и прямой (А1В0). В сечении
этих цилиндров любой плоскостью,
параллельной образующей, получа-
ются равновеликие фигуры — парал-
лелограмм MNN2Mt и прямоуголь-
ник AIQNO\T1M1. Поэтому в силу
принципа Кавальер и и цилиндры ока-
зываются равновеликими:
С другой стороны:
(В2Е— высота наклонного цилиндра).
Из (*) и (**) находим (так как
ВВ,Е « а):
Sa.d.b.c, —Sadbc ¦-jjjj^—Sadbc-cosa,
что и нужно было вывести.
13 Вычисление объемов, принцип Кавальери.
1. Доказать, что площадь эллипса
равна лаб, где а, Ь — полуоси эл-
липса *).
2. Определить объем эллипсоида
вращения, получаемого вращением
эллипса с полуосями а и b около оси,
равной 2а.
3. Доказать, что объем тетра-
эдра (треугольной пирамиды) равен
2
— •Scp .h, где через h обозначено рас-
стояние между скрещивающимися пря-
мыми, на которых лежат противо-
положные ребра тетраэдра, a Scp
есть площадь сечения этого тетраэдра
плоскостью, равноудаленной от этих
двух прямых.
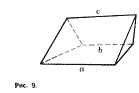
4. Клином называется многогран-
ник, который получится, если концы
*) Об эллипсе см. статью И. Н. Брон-
штейна «Эллипс» в журнале «Квант»
К* 9 за 1970 г.
отрезка, параллельного основаниям
некоторой трапеции,соединить с вер-
шинами этой трапеции, так, как ука-
зано на рисунке 9. Доказать, что
объем клина равен -у (a -f- b -j- с) S±,
где a, b — основания трапеции, с —
длина данного отрезка, a Sx — пло-
щадь треугольника, получаемого при
а
Рис. 9.
сечении плоскостью, перпендикуляр-
ной к ребрам а, Ь, с клина (или его
продолжения вдоль этих ребер).
14 Вычисление объемов, принцип Кавальери.