Решение задач по электростатике
(Потенциал) Г. .Я. Мякишев
Наибольшие трудности в курсе
электростатики вызывает понятие по-
тенциала или разности потенциалов.
Работа электростатических сил
Страница переведена на новый сайт https://myeducation.su/ : страница
ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЖУРНАЛ Квант (6 июнь 1972)
равна изменению потенциальной
энергии, взятой с обратным знаком:
ДЛ = — (Я2 — /7,) = — А/7,
где Пх и /78 — начальное и конеч-
ное значения энергии. Так как ра-
бота пропорциональна силе, а сила,
в свою очередь, пропорциональна
заряду q, на который действует поле,
то энергия заряда в поле П~ц. Сле-
довательно, отношение — не зависит
от заряда и может быть принято за
характеристику, поля. Эта характе-
ристика называется потенциалом:
A)
Отсюда следует, что
= — q (<р, —
B)
Проекция напряженности поля
на произвольное направление, за-
даваемое малым отрезком Д/, связа-
на с разностью потенциалов на кон-
цах этого отрезка формулой
?,« —
Л1
C)
Понятие разности потенциалов
оказывается довольно сложным из-за
того, что работа выражается не через
сам потенциал, а через разность по-
тенциалов (формула B)). Поэтому
добавление к потенциалу любой по-
стоянной не изменит величины рабо-
ты, а значит, и не изменит ничего,
что имело бы физический смысл. По-
тенциал определяется с точностью до
Г. .Я. Мякишев
произвольной постоянной, как и по-
тенциальная энергия *).
Подобно напряженности поля,
величина потенциала зависит от рас-
пределения в пространстве электри-
ческих зарядов. В частности, потен-
циал равномерно заряженной беско-
нечной плоскости в системе СИ опре-
деляется формулой
q>*= -j-x + c, D)
где а — поверхностная плотность за-
ряда, х — расстояние до плоскости,
с — произвольная постоянная. Так
как напряженность поля плоскости
Е ~ —, то формулу D) можно пе-
реписать в виде
Ф = Ех + с. E)
Потенциал точечного заряда мож-
но найти с помощью закона Кулона
и формулы B) для разности потен-
циалов. Но это достаточно сложная
задача. Гораздо проще доказать, что,
взяв потенциал точечного заряда в
•) Это трудно представить себе. Ведь
если мы знаем потенциал в каждой точке, то
тем самым напряженность электрического по-
ля также определена в каждой точке. Но в то
же время потенциал в данной точке может
быть любым, раз он определен с точностью до
постоянной.
Дело здесь в следующем. Потенциал п
точке можно считать равным любому значе-
нию, но изменение потенциала при смещении
из данной точки в другую, сколь угодно близ-
кую, будет вполне определенным, так как
зависимость потенциала от координат
ф (х, у, г) известна. Если потенциал вообще
ие меняется при таком смещении, то в этой
точке поле равно нулю. Зная характер изме-
нения потенциала вблизи произвольной точки,
можно всегда найти величину и направление
напряженности поля в этой точке с помощью
формулы C).
55 Решение задач по электростатике.
виде
Ф—2-.
F)
где с — произвольная постоянная,
можно с помощью B) получить закон
Кулона. Это и будет означать, что
формула F), которая приводится без
доказательства в школьном курсе фи-
зики, действительно определяет по-
тенциал точечного заряда в системе
СГСЭ.
В самом деле, пусть точечный
заряд <7« смещается в поле другого
точечного заряда qx на очень малый
отрезок Дг. Тогда, согласно форму-
лам B) и F),
( L_ _!_Л 4i4
\r -У Л/- r j — гг -f
Так как Аг мало, то г2^гДг и
ДЛ FAr
Дг.
Следовательно, сила F равна -^,
а это и есть закон Кулона. Значит,
формула F) справедлива
Подобно тому как напряженность
поля сферически симметрично заря-
женного шара совпадает с напряжен-
ностью точечного заряда, потенциал
заряженного шара (вне шара) так-
же определяется формулой F). В
системе СИ
Я \-с, G)
если шар находится в однородном
диэлектрике с диэлектрической про-
ницательностью е.
Для решения задач достаточно
хорошо представлять себе физиче-
ский смысл основных формул. Кро-
ме того, часто приходится использо-
вать простые, но очень важные по-
ложения: работа электростатиче-
ского поля на замкнутом пути равна
нулю и все точки проводника в элект-
ростатике имеют один и тот же по-
тенциал.
Задача 1. Может ли сущест-
вовать электростатическое поле, на-
пряженность которого не меняется
56
в направлении х и возрастает в на-
правлении у (рис. 1)?
Решение. Не может, так как
в таком поле работа при перемеще-
нии заряда по замкнутому контуру
Рис. 1.
(например, прямоугольному со сто-
ронами, параллельными х и у) от-
лична от нуля.
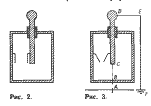
Задача 2. К внутренней стен-
ке изолированного от земли электро-
метра прикреплен металлический
листочек (рис. 2). Стержень и кор-
пус электрометра соединили прово-
дом и после этого сообщили корпусу
электрометра некоторый заряд. От-
клонятся ли при этом листочки элект-
рометра? Что произойдет с листоч-
ками, если провод убрать’ и после
этого стержень соединить с землей?
Решение. Корпус и стержень,
соединенные проводом, будут иметь
Рис. 2.
Рис. 3.
равные потенциалы. Поле внутри
электрометра равно нулю и листочки
не будут отклоняться. После удале-
ния соединительного провода и за-
земления стержня оба листочка от-
клонятся, так как между стержнем
и корпусом возникнет разность по-
тенциалов и, соответственно, элект-
рическое поле. Появление разности
потенциалов очевидно из условия ра-
венства нулю работы электростати-
ческого поля при перемещении заря-
да по замкнутому пути ABCDEFA,
56 Решение задач по электростатике.
Изображенному на рисунке 3. Рабо-
та на участке АС должна быть равна
нулю, так как путь CDEFA прохо-
дит внутри проводника. Следователь-
но, разность потенциалов между кор-
пусом и стержнем равна по величи-
не разности потенциалов между кор-
пусом и землей, которая (поскольку
корпусу электрометра сообщен за-
ряд) не равна нулю.
Задача 3. Чему равна по-
тенциальная энергия П взаимодейст-
вия двух точечных зарядов qt и q2,
находящихся на расстоянии г’ друг
от друга?
Решение. Согласно определе-
нию потенциала A) и формулы для
потенциала точечного заряда F),
Задача 4. Уединенный про-
водящий шар радиуса R несет за-
ряд q. Какова энергия шара?
Решение. Если произвольную
постоянную в формуле G) положить
равной нулю, то потенциал шара
в пустоте
Но собственная энергия шара не
а-
равна т-т-о», как это может пока-
заться вначале.
Энергию шара можно найти, вы-
числив работу, которую нужно со-
вершить для того, чтобы сообщить
шару заряд q. Будем заряжать шар,
перемещая к нему заряд из бесконеч-
ности одинаковыми маленькими пор-
циями. При этом потенциал шара бу-
дет линейно увеличиваться от нуля
Среднее значение потен-
циала -у- г~а . Поэтому энергия ша-
ра оказывается равной
Задача 5. На расстоянии d
от точечного заряда q расположен
незаряженный шар радиуса R. Чему
равен потенциал <р шара?
Решение. Потенциал всех то-
чек шара одинаков. Поэтому для ре-
шения задачи достаточно найти по-
тенциал одной точки шара. Проще
всего найти потенциал центра шара.
Он равен потенциалу, созданному в
центре шара точечным зарядом qj.
ф, = — (произвольную постоянную
d
считаем равной нулю), плюс потен-
циал ф2, созданный зарядами, воз-
никающими на поверхности шара
вследствие электростатической ин-
дукции. Но потенциал <р2 равен’нулю,
так как суммарный заряд на сфере
равен нулю и все элементы наведен-
ного заряда находятся на равном
расстоянии от центра:
Задача 6. Внутрь полой про-
водящей сферы радиуса г, несущей
заряд -\-Qt через маленькое отвер-
стие внесли тело, имеющее заряд —q.
Чему равен потенциал точки, находя-
щейся на расстоянии R>r от центра
сферы.
Решен и е. Поместим вначале
заряд — q в центре сферы. На внеш-
ней поверхности этот заряд индуци-
рует заряд —q, а на внутренней -\-q,
причем заряды распределяются рав-
номерно. Потенциал в точке, находя-
щейся на расстоянии R, равен ф« =
— -~s^~ (так как суммарный потенци-
ал наведенных зарядов равен нулю).
При перемещении заряженного
тела внутри сферы силовые линии
электрического ноля деформируются,
но не проникают сквозь проводящую
поверхность сферы. Поэтому найден-
ное значение потенциала остается
справедливым при любом положении
заряда — q внутри сферы.
Задача 7. В центре проволоч-
ного кольца радиуса R находится за-
ряженная частица, имеющая скорость
и0 (рис. 4). Заряд кольца +Q,
заряд частицы —q. Какую скорость
v будет иметь частица вдали от
кольца?
57 Решение задач по электростатике.
Решение. Потенциал в цент-
ре кольца равен сумме потенциалов,
созданных отдельными элементар-
ными зарядами Дф, на кольце. Так
Упражнения
1. На рисунке 5 изображены эквипотен-
циальные поверхности. Наши направление
электрического поля в точке О.
Рнс. 4.
как заряд Д<2* можно рассматривать
как точечный, то
Потенциальная энергия взаимодей-
ствия заряда —q с зарядом +Q рав-
на
= — qvp = — ¦ qc.
Полная энергия в начальный мо-
мент
В конечном состоянии кинетическая
энергия частицы равна —я-, а по-
тенциальная энергия — qc, так как
зависящее от расстояния слагаемое
потенциальной энергии обращается
в нуль. По закону сохранения энер-
гии
2
Отсюда
Рнс. 5.
2. Металлический шар диаметром 2 .ч
расположен в центре большего помещения
н заряжен до потенциала 10 в. Какое ко-
личество тепла выделится, если шар сое-
динить проводником с землей?
3. Сферическая оболочка радиуса R
заряжена равномерно зарядом Q. Исполь-
зуя закон сохранения энергии, найти рас-
тягивающую силу, приходящуюся па еди-
ницу площади оболочки.
4. N одинаковых шарообразных капе-
лек ртути заряжены одноименными заря-
дами до одного и того же потенциала «| ¦.
Каков будет потенциал ц- большей капли
ртути, получившейся в результате слияния
этих капель?
5. Два заряда по 50 ед. СГСЭ каждый
находятся на расстоянии А?|->ПЮ см друг
от друга. Какую работу надо совершить,
чтобы сблизить их до расстояния R2=5Qcm.
6. Нарисуйте график зависимости по-
тенциала и напряженности поля двух за-
ряженных шариков от расстояния вдоль
линии, проходящей через центры эгнх ша-
риков.
7. Нарисуйте график зависимости по-
тенциала п напряженности поля от рас-
стояния до центра заряженного металличе-
ского шарика радиуса г, окруженного тол-
стон металлической оболочкой, внутренний
радиус которой равен #i (/?,>r), а внеш-
ний — Я*.
Как видите, результат не зависит
от значения постоянной с.
Ответы на кроссворд МФТИ (см. стр. 21)
^..По в с..рт н * ал н:. JL Парта. 2. ‘Лан-
гет,3. Oryj»it 4;. Титан.,6.Вымогательство.
7 Доброжелатель $) Сарафан: 11. Арбатов.
17 Ей-же^ Ш. Изотоп. 19. Басма. 20. Босса.
По горизонтали: 5. Фантасма-
гория. 8. Омета. 9. Забор. 10. Столица.
12. Заноза. 13. Развод. 14. Съем-ка. 15. Ора-
гай. 1С. Негатив. 21. Аврал. 22. Вобла.
23. Импрессионист.
58 Решение задач по электростатике.