ГРАФИК КУБИЧЕСКОГО ЧЕТЫРЕХЧЛЕНА

О. А Жаутыков
Текст, для быстрого ознакомления (в тексте для быстрого ознакомления формулы могут отображаться не корректно):

Страница переведена на новый сайт https://myeducation.su/ : страница

ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЖУРНАЛ Квант (6 июнь 1972)

В «Кванте» № 11 за 1971 год рассказывалось о некоторых
формулах, позволяющих выразить корни кубического уравнения
через его коэффициенты. Однако во многих задачах оказывается
полезным уметь представить себе график «кубического четырех-
члена» . Об этом и идет речь в публикуемой ниже статье.

Поставим своей задачей научить-
ся строить график функции
у = ах3 -г Ьх2 4- сх -г d (а ф% A)
то есть многочлена 3-й степени. Ко-
нечно, можно пытаться построить кри-
вую A) по точкам. Но это слишком
долгий путь, требующий утомитель-
ных вычислений. Мы расскажем о
более простом способе, позволяющем
в каждом конкретном случае легко
представить себе в общих чертах
поседение кривой, описываемой урав-
нением A).
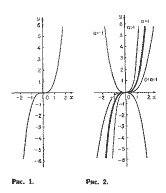
Будем исходить из графика функ-
ции
У = х\ B)
называемого кубической параболойч
Эта кривая строится по точкам
(рис. 1); ее вид необходимо запом-
нить. Она играет при изучении гра-
фика кубического многочлена A) роль,
аналогичную роли параболы у — хг
в теории квадратного трехчлена.
Кубическая парабола обладает
следующими основными свойствами:
1) она симметрична относительно
начала координат и проходит в треть-
ей и первой четвертях (другими сло-
вами, функция B) — нечетная);
2) в начале координат кубическая
парабола пересекает ось абсцисс, од-
новременно касаясь ее.
Легко сообразить далее, как вы-
глядит график функции
C)

где а — действительное число (рис. 2).
Если а > 0, то кривая C) симметрич-
на относительно начала координат
и проходит в третьей и первой чет-
вертях; чем больше а, тем круче ветви
кривой C), чем меньше а, тем они
положе. Например, при а > 1 ветви
кривой C) сильнее по сравнению с ку-
бической параболой B) прижаты к
оси Оу.
При а < 0 график функции C)
симметричен кривой у = \а\хъ от-
носительно оси ординат — он про-
ходит во второй и четвертой четвер-
тях.

26 ГРАФИК  КУБИЧЕСКОГО ЧЕТЫРЕХЧЛЕНА

Наконец, рассмотрим график
функции
у =- ах3 + тх. D)
Его легко построить методом сложе-
ния двух графиков — уже знакомой
нам кривой C) и прямой у — тх,
проходящей через начало координат:
нужно при каждом значении абсциссы
л* сложить соответствующие ординаты
кривой C) и прямой у — тх.
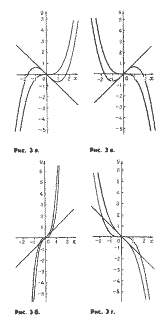
Ясно, что вид графика функции D)
зависит от знаков чисел пит. Имен-
но, если й > 0 и т < 0, то кривая D)
имеет вид, показанный на рисунке 3 а,
если же а > 0 и т > 0, — то вид,
изображенный на рисунке 3 б. Гра-
фик функции D) в случае а < 0 и
т > 0 (рис. 3 в) получается зеркаль-
ным отображением относительно оси
ординат кривой, изображенной на
рисунке 3 а, а в случае а<0ит<0
(рис. 3 г) — зеркальным отображе-
нием кривой на рисунке 3 б; впро-
чем, на рисунке 3 г мы увеличи-
ли о, и парабола стала круче, со-
хранив, однако, общий вид.
Основные свойства кривой D) сос-
тоят в следующем:
1) она пересекает (в начале ко-
ординат) прямую у — тх, одновре-
менно касаясь ее;
2) если числа а и т одного знака,
то эта кривая лишь в начале коор-
динат пересекает ось абсцисс; если же
числа а и m разных знаков, то эта
кривая трижды пересекает ось абсцисс
(в точках х — 0 и х ¦-
-V—-•)¦
Итак, график функции D) мы
рисовать научились. Л теперь пока-
жем, что для любой функции типа (I)
всегда можно найти такие (действи-
тельные) числа т, k, Л, что график
функции A) получается смещением
кривой D) на Л влево и на k
вниз.
В самом деле, если перенести
кривую D) на Л влево и на k вниз, то
получится кривая, описываемая урав-
нением
у -г k = а (х + ЛK + m (х + h).

Этот, многочлен будет совпадать
с многочленом A), если b ~ 3ah,
с ¦- ЗяАа -I- /я, d =- oft3 -i- /«Л — Л,
то есть если числа А, т и к положить
равными
Следовательно, графиком функ-
ции A) служит кривая D), где числи ш
берется из E), смещенная на h влево,

27 ГРАФИК  КУБИЧЕСКОГО ЧЕТЫРЕХЧЛЕНА 

если h > 0, или на \h | вправо, если
/i< О, и на k вниз, если k>0, или
, и на k вниз, если k>0, или
на \k | вверх, если k<Q, где числа h
определяются по формулам E).
ример Построить график
\ |
k оп
Пример. Построить график
функции // — х3 — 4х2 — Ах -\- 16.
По формулам E) находим:
Поэтому нам нужно построить гра-
фик функции
•^**
(рис. 4 а), а затем передвинуть его
4
на— вправо вдоль оси абсцисс и на
160 , . -,
— пверх вдоль оси ординат (рис. 4 б).

АРМЯНСКИЕ  НАРОДНЫЕ ЗАДАЧИ

(Письмо читателей)
Дорогая редакция!
У нас в школе уже 2-й год
действует математический
клуб *ХУ7л (X — труд, Y —
знания, Z — народный фоль-
клор). В основном клуб соби-
рает народные задачи, кото-
рые в Армении называются
«храхчанаканамн». А их
много…
Армянские математики Ана-
ния Ширакаци(УП в.), Мхи
тар Ерзнкаци (XIV в.), Зака
рия Саркаваг (XVII в.) и дру-
гие в своих работах предла-
гали разные «храхчаиа
каны».
…Члены клуба «XYZ»
собрали и отредактировали
более 15 задач — храхчана
кано» из нашего села. Неко-
торые из них мы предлагаем
вашему вниманию.

Камень затянули во двор
Во время строительства
Ваанаванка *) везли из ка-
меноломни двухсотпудовый
камень. Полдороги четыре
быка везли его три дня.
Камень был тяжелый, при-
шлось его разбить, от него
осталось 150 пудов, а быков
взяли иа половину больше,
чем было. Сколько времени
камень тянули во двор
Ваанаванка?
Сто марзан пшеницы
Мельник разделил 100
марзан пшеницы на три час-
ти, чтобы погрузить на ло-
шадь, осла и ослика. Если
от груза лошади отнять один
груз осла, то остаток ослик
может перевезти в шесть
приемов, а если отнять два
груза осла, то остаток ослик
может перевезти в четыре
приема, а на пятый — оста-
нется груз, на половину мень-
ший, чем в каждый из пре-
дыдущих четырех.
Узнайте,
мсльньк
лошадь, осла и ослика?
сколько груза
погрузил на
*) Ваанаванк—известный
армянский монастырь X
века.
Дочери Навасарда
Дочери Навасарда были
ковроткачихамн. Если бы
Навасард дал каждой до-
чери по семи мотков ниток
Г«з одного, то у него еще
осталась бы такая же доля
мотков. А Сели бы он дал
каждой по семи и еще одному
мотку, то дочке «Заре ниток бы
не досталось совсем. Сколь-
ко мотков ниток было у
Навасарда и сколько доче-
рей?
Лиса и лисята
На семи горах растут по
сечь деревьев, под каждым
деревом — семь нор, в каж-
дой норке живет семь ли-
сиц, у каждой лисицы семь
лисят. Сколько всего ли-
сиц?
Роберт Эджананский
Клуб *XYZ» Лернадэорской
восьмилетней школы
Кафанского района
Армянской ССР

28 ГРАФИК  КУБИЧЕСКОГО ЧЕТЫРЕХЧЛЕНА

 

ГРАФИК КУБИЧЕСКОГО ЧЕТЫРЕХЧЛЕНА