§ 6. Статика.
Страницы переведены на новый сайт:
СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ
https://myeducation.su/sbornik-zadach-po-elementarnoj-fizike/
На неподвижный цилиндр намотана нить, длина ко
торой 1—RQ, где R — радиус цилиндра, § — угол в радианах
между радиусами, проведенными в.начальную и конечную
точки касания нити с цилиндром. Один конец нити
тянут с силой Г*. Коэффициент трения между нитью и поверхностью
цилиндра равен к. Определить силу натяжения
второго конца нити, если известно, что это максимальная
сила, при которой еще отсутствует проскальзывание.
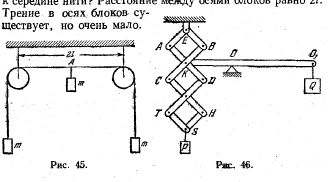
123. На концах лити, перекинутой через два блока, висят
два одинаковых груза (рис. 45). На какое расстояние
опустится третий груз той же массы, если его прикрепить
к середине нити? Расстояние между осями блоков равно 21.
124. Равнобедренный клин с острым углом а забит в
щель. При каких значениях угла а клин не будет вытолкнут
из щели, если коэффициент трения между клином и материалом
щели равен k?
125. Каково соотношение между грузами Р и Q, если
известно, что система, изображенная на рис. 46, находится
в равновесии? Длина стержней AD, ВС, СН, D T и длина
плеча ООх в два раза больше длины стержней АЕ, ЕВ, TS,
SH и длины плеча КО соответственно. Весом стержней и
рычага пренебречь.
126. Для того чтобы сдвинуть прямоугольный ЯЩИК
длины I и высоты h, к его верхнему ребру перпендикулярно
грани прикладывают горизонтальную силу /.’Какую вели-
чину должен иметь коэффициент к трения между ящиком
и полш, чтобы ящик сдвинулся не шрокндьшаясь?
Трение в осях блоков существует,
но очень мало.
31 Статика.
127. Однородная балка, вес которой Р, лежит на полу.
Коэффициент трения балки о пол равен k. Что легче: повернуть
балку в горизонтальной плоскости относительно ее
центра или перемещать балку поступательно? В обоих случаях
балку двигают два человека.
128. Мостовой кран, вес которого Р—2Л0* Н, имеет
пролет L —26 м (рис. 47). Трос, на котором подвешен груз,
находится на расстоянии /=10 м от одного из рельсов,
Определить силы давления крана ца рельсы, если он поднимает
груз весом jP,M0* Н с ускорением а=9,8 м/с8.
129. Рычаг изогнут так, что стороны его АВ, ВС и CD
равны между собой и образуют друг с другом прямые углы
(рис. 48). Ось рычага—в точке В. Перпендикулярно плечу
рычага АВ в точке А приложена сила Р. Определить минимальнее
значение силы, которую нужно приложить в
точке D, чтобы рычаг находился
в равновесии. Весом
рычага пренебречь.
130. Между двумя одинаковыми ящиками, стоящими на
полу, вставлена палка, немного не доходящая до пола
(рис. 49). К верхнему концу палки приложена горизонтальная
сила. Какой из ящиков сдвинется раньше?
131. Тяжелый однородный шар подвешен на нити, конец
которой закреплен на вертикальной стене. Точка прикрепления
нити к шару находится на одной вертикали с
32 Статика.
133. Для подъема тяже-
цилиндричеекого катка
туса R на прямоугольную
яеньку пришлось прило-
к его оси горизонтально
направленную силу, равную весу катка. Определить
ивзсимальную высоту ступеньки.
134. На двух наклонных плоскостях, образующих с
циэонтом углы а!=30° и а * = 60“ , лежит шар весом Р.
делить силы давления шара на каждую из плоскостей,
I известно, что трение между шаром и одной из плоскостей/
сутствует.
«135. На передней стенке ящика шкафа имеются две сим-
рично расположенные ручки. Расстояние между руч-
/, длина ящика а. Коэффициент трения между ящиком
равен k. Всегда ли можно выдвинуть ящик из
1, прикладывая только к одной ручке силу, перпен-
улярную стенке ящика?
136. На шероховатом, / горизонтально расположенном
однородная доска (рис. 51). После
того. кзк утяжелили один из ее
Концов, обнаружилось, что равновесие
достигается, когда доска составляет
угол а с горизонтом. Каков
коэффициент трения между доской
и бревном?
137. Верхний конец лестницы
опирается на гладкую вертикаль-
стену, а нижний конец лестницы стоит на шерохо-
йолу . Коэффициент трения между лестницей и полом
dfe. Определить, при каком значении угла, а между
лей и стеной лестница будет находиться в равновесии.
—ЛЗД. Решить предыдущую задачу в предположении,
стена не гладкая к коэффициент трения между леетни-
и стеной также равен k.
33 Статика.
139. Однородная тонкая палочка АВ длиной I лежит горизонтальной поверхности стола. К концу В палочки пр*
креплена нить длиной 21 (рис. 52). Как будет двигаться т
лочка, если другой конец нити С медленно поднимать вдол
неподвижной вертикально
прямой DO, проходящей ч<
рез конец А палочки? Веса
нити пренебречь.
140. При каком значени)
коэффициента трения человен
бегущий по прямой твердо!
дорожке, не может поскольз
нуться? Максимальный угои
между вертикалью и линией
соединяющей центр тяжесл
бегуна с точкой опоры, ра
вен а.
141. К гладкой вертикальной стене дома прислонеж
лестница. Угол между лестницей и горизонтальной Поверх
ностью земли а=б0°. Длина лестницы I. Центр тяжести е<
находится посередине. Как направлена сила, действующа!
на лестницу со стороны земли?
142. Лестница, центр тяжести которой находится посе
редине, опирается на абсолютно гладкие пол и стену
Рис. 52.
(рис. 53). Каким должно
было бы быть натяжение
веревки, привязанной к середине
лестницы, чтобы
удержать ее от падения?
143. По лестнице, прислоненной
к гладкой вертикальной
стене, поднимается
человек. Лестница начинает
скользить лишь тогда,
когда человек поднялся на
определенную высоту. Почему?
144. Картина подвешена
к вертикальной стене с
Рис. 53
помощью шнура АС длины I, образующего со стеной угол
а. Высота картины ВС- d (рис. 54). Нижняя часть картины
не закреплена. При каком значении коэффициента
трейгя между картиной и стеной картина будет в равновесий?
34 Статика.
145. Четыре однородных стержня шарнирно скреплены
друг с другом в точках В, С и D (рис. 55). Два крайних
стержня АВ и DE могут свободно вращаться относительно
неподвижных точек А и Е, расположенных на горизонтальной
прямой. Длины стержней попарно равны, AB—ED
и BC—CD. Массы стержней одинаковы. Показать, что
при равновесии углы а и р связаны соотношением
tga = 3tg(5.
146. Чему равен коэффициент трения между полом и
ящиком весом в 100 Н, если наименьшая сила, необходимая
для того, чтобы сдвинуть ящик с места, составляет 60 Н?
147. На цилиндр массы т намотана невесомая нерастяжимая
нить (рис. 56). С какой наименьшей силой ^min
и под каким углом а± к горизонту нужно тянуть эту нить,
чтобы цилиндр, вращаясь, оставался на месте?
Коэффициент трения между цилиндром и полом равен k.
148. На рис. 57 изображена упрощенная схема паровой
мащйньр и кривошипно-шатунного механизма паровоза.
Рис. 57, а и б соответствуют моментам, когда пар находится
а) 6)
Рис. 57.
я левой и правой частях цилиндра соответственно. Рассчитать
силу тяги для этих случаев в момент, когда точка А
лежит ш одной вертикали с осью ведущего колеса. Давление
пара в цилиндре р, площадь поршня S, радиус ведущего
35 Статика.
колеса R, а расстояние ОА=*г. Массой кривошипно-шатунного
механизма, поршня и ведущего колеса пренебречь.
149. Кирпичи укладывают друг на друга без связующего
вещества так, что часть каждого последующего кирпича
выступает над нижележащим (рис. 58). На какое максимальное
расстояние правый край верхнего кирпича может выступать
над правым _ краем самого
нижнего кирпича, служащего основанием
всей кладки? Длина каждого
кирпича I.
150. Найти центр тяжести тонкой
однородной проволоки, .согнутой в
виде полуокружности радиуса г.
151. Определить положение центра тяжести однородного
тонкого полукруга радиуса г.
152. Определить положение центра тяжести тонкой однородной
проволоки, изогнутой по дуге радиуса г (рис. 59).
Рис. 58.
Рис. 59. Рис. 60. Рис. 61.
153. Определить положение центра тяжести тонкой однородной
пластинки, вырезанной в виде сектора радиуса г,
имеющего центральный угол а (рис. 60).
154/ Определить положение центра тяжести тонкой однородной
пластинки, представляющей: собой прямоугольник
со сторонами г и 2г, из которого вырезан полукруг радиуса
г (рис. 61).
36 Статика.
§ 6. Статика. Ответы.
122., Рассмотрим часть нити,, прилетающую кцилиндру. Разобьем
угол 0 на большое число я частей и обозначим 0/я 5= а- Представши,
нить как п связанных между собой кусочков,.и выделим /-й-ку-
сочек (рис. 322). На него действуют
соседние- части, нити, с. силами Ту в
Ту+li реакция*. ц и л и н д р а> и сила ф е нии
hNj,. Учтя* что угол; а мал,, полу—
чим следующие уравнения равновесия:
TJ+1—Tj — kNf = Q,
, Nj — Тусс/2 — Ту м а /2 0.
Отсюда 7у+1 = Ту(I-f~fta>, т, е,
Т’1 = Т’0(1+йа),
Г2 = Г1 (1 + * а ) , . . . ,
СледбватеяБно, Tn = Tj ( I + kit)4 = Та (1 -f kQ/n)*, и при /г->-a>
получим
Т = . lira Г„ = Ига Го (14-А0/п)в = 7 ,ое40, П -+-<е
где е —2,71828… —основание натуральных логарифмов.
123. В’ положении равновесия (рис. 323) mg—2mgcos a = 0 .
Следовательно, a =60°.. Искомое расстояние^ h = l ctgM=l/y~3.
Равновесие установится, после того, как- затухнут колебания-, возни*
кающие при опускании груза,
124. Равенство проекций сил на напрааление вертикалн (рис. 324)
приводит к уравнению
2N sitr(oi/2)—2/?Tp cos (a/2) F=0,
203 Статика. Ответы.
^(Массой клина обычно можно пренебречь.) Следовательно, tg(a/2)<ft
и a < 2 arctgft.
125. Если груз Р опустится на высоту h, то точка К опустится
на 1/3h. Груз Q при этом поднимается на i/3h. Применяя «золотое»
правило механики, имеем Ph=Q2/3h. Отсюда P = 2/sQ-
126. Если ящик не опрокидывается, то момент силы F, вращающий
его против часовой стрелки вокруг ребра при основании, меньше
или равен моменту силы тяжести, вращающему ящик по часовой
стрелке. Чтобы ящик скользил, сила F должна быть больше максимальной
силы трения, приложенной к ящику. Следовательно,
Fh<mgl/2, F ^ kmg. Отсюда ‘
127. Для поворота балки необходимо, чтобы момент сил, приложенных
к концам балки, был больше момента сил трения, когда эти
силы достигают своего максимального значения. Силы трения распределены
равномерно вдоль балки (рис. 325). Среднее плечо сил
О
I I ш И И
Рис. 325.
трения, действующих на левую или правую часть балки, равно //4,
если длину всей балки обозначить через I. Момент всех сил трения
относительно центра балки равен 2(кР/2) (1/4). Следовательно, для
поворота балки необходимо, чтобы приложенные силы F удовлетворяли
неравенству 2FI/2 > kPl/4. Отсюда F > кР/4. Для поступательного
перемещения балки необходимо, чтобы 2F > kP. Следовательно,
балку легче повернуть.
128. Уравнение, движения груза имеет вид P0a/g= F— Р„
(рис. 326). Сумма сил, действующих на кран по вертикали, равна
нулю. Поэтому P1-\-P3 = P-\-F. Равенство нулю суммы моментов
сил относительно точки А дает уравнение Fl-\-PL/2 = LP3. Решая
данную систему уравнений, найдем
Pj и 2,23-10* Н, Р2 « 1,77-10« н .
204
129. Для равновесия рычага приложенная к точке D сила
должна создать момент, равный Р-АВ. Сила будет минимальной
при максимальном плече, равном BD. Следовательно, F=±P-AB/BD=
= Р/ У 2 и направлена перпендикулярно BD.
130. Если трение между полом и ящиками отсутствует, то
ящики сдвинутся одновременно. Если же коэффициент трения не
равен нулю, то раньше сдвинется правый ящик (см. рис. 49), так
как сцла, приложенная к нему со стороны палки, будет больше,
чем сила, приложенная к левому ящику. Действительно, со стороны
правого ящика на палку действует сила Ft, направленная против F,
а со стороны левого ящика—сила F2, направленная по F. Сумма
сил при равновесии равна нулю. Следовательно, F1 = F-\-F2, и
сила Ft раньше, чем F2, достигнет значения максимальной силы
трения покоя.
131. Равенство нулю суммы моментов сил, действующих на шар,
относительно точки А (рис. 327) приводит к уравнению
f Ip7?-7V7? = 0.
Так как ETp<feiV, то ftissl.
132. Для того чтобы тело находилось в покое, необходимо,
чтобы суммарный момент сил, стремящийся повернуть тело по часовой
стрелке, был равен моменту сил, стремящемуся повернуть тело
против часовой стрелки вокруг какой-либо точки (например, вокруг
центра тяжести). В данном случае момент сил трения, вращающий
кирпич по часовой стрелке, должен быть равен моменту сил давления
плоскости на кирпич. Отсюда следует, что сила давления плоскости
на правую часть кирпича должна быть больше, чем на левую.
По третьему закону Ньютона и сила давления правой половины
кирпича на плоскость должна быть больше силы давления левой.
133. Для того чтобы каток поднялся иа ступеньку, необходимо,
чтобы момент сил, вращающих каток вокруг точки А (рис. 328)
против часовой стрелки, был бы по крайней мере равен моменту
сил, вращающих его по часовой стрелке:
Р(/?—Л) = 7> У R2—(7? — А)а.
Отсюда й = (2 ± У 2)R/2. Так как h < R, то
Л = (1- У 2/2) R » 0,297?.
205
134. Так жак на одной из плоскостей сила трения -равна нулю,
ло она равна нулю и «а другой плоскости. В противном случае шар
-вращался бы вокруг -своего центра, ибо момент всех остальных сил
относительно этого центра .равен нулю {ввиду равенства нулю плена
каждой ,из этих сил относительно центра шара). Суммы проекций
Рис. 328.
сил на вертикальное и горизонтальное направления равны нулю
(рие. 329). Поэтому
iVxcos о*— JV2 cos а х = О, Р — Wx-sin а 2 — Af2 sin а х = О,
где Nx и N2— искомые силы давления. Отсюда
N, Р Р ’ sin <*2+ cos a 2- tg a x * N« = sin a x -f- cos ox • tg a 2 ‘
435. ^Обозначим через :’F силу., приложенную к одной ручке.
Из-за действия силы г произойдет поворот ящика, вследствие чего
возникнут в точках А и В упругие силы /Vx и jV2 (рис. 330), действующие
на ящик со стороны шкафа. Зги приложенные к ящику
Рис. 330.
силы равны друг яругу: jVx = N2— N. Из условия равенства, нулю
момента всех действующих сил относительно центра ящика С следует,
что N = Flj2a. -Ящик может -быть выдвинут, если приложен
206
ная, сила F больше, максимальней силы трения, покоя: F > /i,-|-/2.=
= 2kN. Для того чтобы последнее неравенство, выполнялось,. необходимо,.
чтобы k < af l.
136. Доска, отклоненная, на угол а. от. горизонтального положен
ния на. шероховатом бревне, аналогична, телу,, удерживаемому силами
трения на наклонной плоскости, с углом при основании, а. Поэтому
при равновесии Fxp = mg sin а. Учитывая, что FTp< femg cos а,
имеем tgoc<fe. , —
137.. Силы, приложенные к лестнице, изображены на рис. 331..
В случае равновесия суммы проекций сил вдоль вертикали и горизонтали
равны нулю. Следовательно, Mi = FTp, Ni = mg. Равенство
нулю суммы моментов сил относительно точки В дает еще одно
уравнение: ‘ ■ .
Отсюда FTp = (mg tg a)/2. Таю как сила- трения удовлетворяет неравенству
kN2, то для равновесия получаем следующее необходимое
и достаточное’ условие; tga«g;2&.
1381- Приложенные к лестнице силы1 изображены на; рис;. 332.
Из1 условия равенства; нулю* суммы; сил? и сумма? моментов- сил; имеем
Силы трения / и Fxp удовлетворяют неравенствам /<&/7х и Fxp<&V2.
Используя, первое неравенство и уравнения” (1) и (3), получаем
ctga>s^N2/2Ni — k/2. Так как k ^ sN JN 2, то c tg ag s (1 — k2)/2k. Введя
обозначение £ = tg(i, данному нера- о
вевсгву можно придать более удобную ,
для вычислений форму: ctg a 3* ctg 2$, Г
или a-sS, 20. Т
. Рис. 332. Рис. 333.
1-39; Если- в момент, когда; конец палочки. В начнет приподниматься,
.значение, силы* трения Егр^ ,Ш окажется достаточным для
■юта; чтабжгконец А не. проскальзывая,, то паяочиа? начнет: вращаться
вокруг точки А. В противном, случае конец Л начнет скользить до тех
пор, пока сила трения FTp=&V не. окажется, способной удержать
207
вокруг конца А.
Найдем, какие значения должен иметь коэффициент трения к,
чтобы скольжение прекратилось при определенном угле а между
палочкой и нитью. Равенство сил в момент, когда палочка почти
горизонтальна, приводит к уравнениям
~ FTp= 7 ’ cosa, P — N + T sin a.
Равенство моментов сил относительно точки А запишется следующим
образом:
Р(/2 = 77 sin a.
Используя данную систему уравнений, найдем
* = f Tp/iV = ctga.
Для того чтобы палочка вообще не начала скользить, необходимо,
чтобы /s ^ c tg 6 0 o= i / |/~ 3 .
140. Сумма моментов сил, действующих на человека относительно
его центра тяжести, равна нулю. Поэтому сила F, действующая со
стороны земли, обязательно направлена к центру тяжести человека С
(рис. 334). Горизонтальная составляющая этой силы не может быть
больше максимальной силы трения покоя: F sin а <; kF cos а. Отсюда
feSstga.
141. На лестницу действуют сила тяжести Р, сила F со стороны
земли и реакция опоры N. Так как стена гладкая, сила N (рис. 335)
перпендикулярна ей. Направление силы F проще’ всего определить,
если найти точку, относительно которой моменты сил Р и N равны
нулю. Такой точкой будет точка пересечения прямых ON и ОР.
Тогда и момент силы F относительно этой точки тоже должен быть
равен нулю. Следовательно, сила должна быть направлена таким
образом, чтобы ее продолжение прошло через точку О. Как вытекает
из рис. 335, направление силы F составляет с лестницей угол
Р = 30°—arctg(l/2 У 3) я 14°10′. Сила, действующая на лестницу
со стороны земли, будет направлена вдоль лестницы только в том
208
случае, если все остальные силы будут приложены к центру масс
лестницы или же будут действовать вдоль нее.
142. Лестницу нельзя удержать от падения с помощью веревки,
привязанной к ее середине. Моменты сил реакции пола и стены, а
также момент силы натяжения веревки относительно точки О равны
нулю при любом натяжении Т (рис. 336). Момент силы тяжести
относительно той же точки отличен от нуля. Поэтому лестница обязательно
упадет.
143. Со стороны стены на лестницу действует реакция Mf, перпендикулярная
стене. На нижний конец лестницы действуют силы N2
(реакция опоры) и FTp (сила трения) (рис. 337).
Если для простоты не учитывать массу лестницы,
то кроме этих сил на нее действует еще вес
человека Р. Равенство проекций сил по горизонтали
и вертикали дает М2 = Р и N1 = Frp.
Пусть вначале человек находится в нижней части
лестницы (точка А). Равенство моментов сил относительно
точки О приводит к уравнению МгСВ =
= P cos а-АО. Следовательно, чем выше находится
человек, тем большее значение будет иметь сила
N±. Но Ртр = М1. Поэтому и сила трения, удерживающая
лестницу, растет по мере того, как человек
поднимается вверх. Когда Рхр достигнет своего
максимального значения, равного kP, лестница
начнет скользить.
144. При равновесии сумма сил, действующих
на картину (рис. 338), равна нулю. Следовательно,
^’ = Ртр+ Т cos a, N = T sin а . Сила трения должна
удовлетворять неравенству Ртр< £М или k 3
моментов относительно точки В дает уравнение
: Ртр/М. Равенство
-к- / sin а = Т (/ cos а -f У d2—l2 sin2 а) sin а.
209
стержень
ВС действует на стержень CD. Предположим, что у этой силы
имеется вертикальная составляющая, направленная вверх. Тогда по
третьему закону Ньютона стержень CD действует на стержень ВС
с силой, у которой вертикальная составляющая направлена вниз.
Однако- это противоречит симметрии задачи. Следовательно,, вертикальная
составляющая силы / должна быть равна нулю. Сила; действующая
на стержень CD со стороны стержня DE, будет иметь и
горизонтальную и вертикальную составляющие*, как. указано- на
рис. 339, а.
Из, равенства нулювсехсил, дейстаующих на CD. следует, что
F s=mg и / = /’. Равенство нулю момента сил относительно D дает
/ sin Р • CD = mg CD (cos P)/2,. или tg (5—mg/2/.
На рис. 339,6 изображены силы, действующие на стержень DE.
Из условия равенства нулю момента сил относительно Е вытекает
/ sin а • DE — F cos-а..-DE-\~rng-° ~ ^ ВЕ, или ig.a, = ^ ~ .
«Следовательно, tg a = 3 tg f$ .
146. Действующие на, ящик силы, изображены. на,рис. 340. Условия
равновесия имеют вид,Q c o s — и. P=M+Q?sin,a. В.момевт
нарушения равновесия сала трения-, достигает, максимальной величины
Отсюда Q =kP/(cos a-f-fe.sin а.}. Величина Q будет
минимальной. при значении, угла, а, соответствующем максимуму
знаменателя дроби. Для нахождения максимума преобразуем знаменатель,
введя вместо к новую величину ф, так что tg ф —
Тогда c o sa -+ * s in u = c o s (а —ф)/созф, или cos a+ fe sin a =
210
= }/~l +&2cos ( a —tp). Так как максимальное значение cos ( a—ср)
равно 1, то Qmin1= ЬР/ V [-{-№. Отсюда k= Q[V~P2— Q2 = 0,75.
147. Силы, .действующие на цилиндр, изображены на рис. 341.
Так как цилиндр поступательно не движется, то
тр -F cos.a=0, Fsin a —jwg+jV = 0.
Сила трения Fxp—fcV. Отсюда F = kmg/(cos a + fe sin a). Знаменатель
этого выражения можно представить в виде Л sin (a-f-ф), где
А — у1 l-j-fc*. Следовательно? минимальная сила, с:которой нужно
\\ SУ t FT p У////////////У/У. уУ/Л^/У/УУ/УУ/.
Фис. 341.
тянуть: нить, Fmtn=sfemgrAl/ft+fe2. Угол а? найдется из уравнение,
cos + 6 sin a j = 1 -f-#2, откуда tg’ a, —k.
148. Силы, действующие на поршень и заднюю крышку цилиндра,
равны F1 = F2 = pS (рис. 342, а). На точку колеса А в горизонтальном
направлении действует также сила F2, передаваемая от поршня
через кривошипно-шатунный механизм.
Сумма моментов сил, действующих на колесо, относительно его
оси равна нулю. (Массой колеса мы пренебрегаем.) Следовательно,
FTpR = F2r, где F xp—сила трения. Так как сумма сил, действующих
на колесо, также равна нулю, то сила F8, действующая ва ось со
стороны подшипников паровоза, равна F3 = Fxp+ F a. Но третьему
закону Ньютона на паровоз со .стороны оси действует сила F4= F 3.
Следовательно, сила тяги F = F 4-—:F1= F Tp-==pSf//?.
. Во .втором положении поршня и кривошипно-шатунного механизма
интересующие нас силы изображены на рис. 342, 6 .F ^p~ F 2rjR
по тем же соображениям, что и в предыдущем случае. Сила тяги
F = F ,—F4 = Fxp == pSr/R. -Как и гследевяло ожидать, сила тяги
равна силе трения, ибо сила трения-
действующая-на паровоз.
211
149. Наибольшая длина выступающей части самого верхнего
кирпича равна I/2. Центр тяжести двух верхних кирпичей С2 на-
ходится на расстоянии 1/4 от края второго
кирпича (рис. 343). Следовательно, на
эту длину второй кирпич может быть выдвинут
относительно третьего.
Центр тяжести трех верхних кирпичей
t -р*
• f
-з определяется равенством моментов сил
■2Р
тяжести относительно С3: Р (1/2—х) = 2Рх.
Отсюда х = //6, т. е. третий кирпич может
выступать над четвертым не более чем на
t/б. Аналогично можно найти, что четвертый
кирпич выступает над пятым на 1/8, и
т. д. Характер изменения длины выступающей
части с увеличением числа кирпичей
очевиден. Максимальное расстояние, на
которое правый край верхнего кирпича может выступать над правым
краем кирпича, служащего основанием, записывается в виде
ряда
Ж
Рис. 343.
40 1
При неограниченном увеличении числа кирпичей эта сумма стремится
к бесконечности. Действительно, сумма ряда
1+ т + т + т + т + ■ g ■ + y + ■§г+••,
больше суммы ряда
t/ 2 1/2
1 + т + т + т + ‘ § ‘ + 4 + 4 + — § — + • • •»
а эта последняя сумма заведомо бесконечно велика в случае бесконечного
числа членов. Центр тяжести всех кирпичей проходит через
правый край самого нижнего кирпича. Равновесие будет неустойчивым.
(Данная картина имела бы место в случае, если бы Земля
была плоской.)
150. В окружность радиуса г впишем правильный многоугольник
(рис. 344). Найдем далее момент (относительно оси АК) сил тяжести,
приложенных к серединам сторон многоугольника АВ, ВС, CD, DE
и т. д., считая, что сила тяжести действует перпендикулярно чертежу.
Этот момент равен рg (ABxl-\-BCx2Jt-CDx3~\-DExi -\-EFxi -\-FKx6),
где р —масса единицы длины проволоки.
Рассматривая подобие соответствующих треугольников, можно
показать, что произведения ABxt , ВСхг, CDx3 и т. д. равны соответственно
AB’h, B’C’h, C’D’h и т. д., где А —апофема многоугольника.
Таким образом, момент равен
pgh (А й ‘+ В ‘С -f- C’D’ + D’E’ + E’F’ + F’K) = pgh2r.
Если число сторон безгранично возрастает, то величина h стремится
212
произведению
силы тяжести проволоки iirpg на расстояние х центра
тяжести от оси АК. Итак, 2r2pg= nrpgx, откуда х= 2 r jn .
Рис. 344.
151. Разбиваем полукруг на треугольники и сегменты, как
показано на рис. 345. Центр тяжести треугольника лежит, как
известно, на пересечении медиан.
В данном случае центр тяжести
каждого треугольника находится
на расстоянии 2/3h от точки О
(h—апофема). При безграничном
увеличении числа сторон центры
тяжести треугольников будут лежать
на окружности радиуса 2/зг,
а площади сегментов будут стремиться
к нулю. Таким образом,
задача сводится к тому, чтобы определить
центр тяжести полуок- v
ружности радиуса 2/3г. Из решения задачи 150 следует, что х —
расстояние центра тяжести полукруга от точки О—равняется
__2 2_ . 4
Х~ я 3 Г~ Зя Л
152. Применяя метод, изложенный в решении задач 150 и 151,
можно показать, что центр тяжести находится в точке С, располо-
женной на расстоянии СО= 2 sin (а/2)- г от центра кривизны дуги
(см. рис. 59).
153. Используя решения задач 150, 151, 152, можно показать,
что центр тяжести находится в точке С, отстоящей от точки О на
расстояние пС О=-4^ -s-i-n— (^а—/2)- г .
154. При определении положения центра тяжести пластинку с
вырезом формально можно рассматривать как сплошную, если
213
считать:, что’ на нее’ наложен гголукруг отрицательной массы, равной
по величине массе вырезаемой- части.. Момент сил тяжести положительной
и отрицательной масс относительно оси, АВ равен-
еслй сила «жести, действует перпендикулярно чертежу, р —масса
единицы площади пластинки (см. решение задачи 151).» С другой
стороны, этот момент равен произведению силы тяжести пластинки
на расстояние х = ОС от центра ее тяжести’до оси АВ. Следова-
214 Статика. Ответы.