§ 9. Закон всемирного тяготения.
Страницы переведены на новый сайт:
СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ
https://myeducation.su/sbornik-zadach-po-elementarnoj-fizike/
Почему Земля сообщает всем телам одно и то же
ускорение независимо от их массы?
229. Найти величину и размерность в системе СГС
гравитационной постоянной, принимая во внимание,
что средний радиус Земли /?=6,4* 108 см, а масса Земли
М=6-10” г
ЗАДАЧИ ПО ФИЗИКЕ.
Свойства пара.
М=6-10” г.
230. При каких условиях тела внутри космического корабля
будут находиться в так называемом состоянии невесомости,
т. е. перестанут оказывать давление на стенки кабины
корабля?
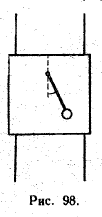
231. Легкий маятник, состоящий йз стержня и диска
(рис. 98), укреплен на деревянной рамке, которая может
свободно падать вдоль направляющих проволок.
Маятник отклонили от положения’
равновесия на угол а и отпустили. В момент,
когда маятник проходил крайнее
нижнее положение, рамку перестали удерживать,
и она начала свободно падать. Как
будет двигаться маятник относительно рамки?
Трением и сопротивлением воздуха
пренебречь.
232. Планета движется по эллипсу, в
фокусе которого расположено Солнце. Принимая
во внимание работу силы тяготения,
Рис. 98. указать, в какой точке траектории скорость
планеты будет максимальной и в какой
— минимальной?
233. Искусственный спутник Земли движется на высоте
й—670 км по круговой орбите. Найти скорость движения
спутника.
234. Как изменяется со временем скорость искусственного
спутника Земли при движении его в верхних слоях
атмосферы?
235. По круговой орбите на небольшом расстоянии друг
от друга в одном направлении движутся два спутника.
G первого спутника на второй нужно перебросить контей-
‘ нер. В каком случае контейнер быстрее достигнет
второго спутника: если его бросить по движению первого
спутника иди против движения? Скорость контейнера
относительно спутника и много меньше скорости спутника
о.
52 СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ. Закон всемирного тяготения.
236. Оценить массу Солнца М, зная, что средний радиус
орбиты Земли /?=149-1Q* км.
237. Определить минимальное удаление h от поверхности
Земли первого искусственного спутника, запущенного в
СССР 4 октября 1957 г., если известны следующие данные:
максимальное удаление спутника от поверхности Земли-f
Н = 900 км; период обращения спутника вокруг Земли
Т —96 мин; большая полуось лунной орбиты #=384 400 км;
период движения Луны вокруг Земли Т —27,Ъ суток и радиус
Земли :Rv=6370 км.
238. В воде имеется пузырек воздуха радиуса г и железный
шарик того же радиуса. БуДут ли они притягиваться
•другк другу или отталкиваться? Какова величина силы
Взаимодействия между ними? Расстояние между центрами
шарика и пузырька равно #.
239. В воде имеется два пузырька воздуха радиуса г.
Притягиваются или отталкиваются пузырьки? Какова
величина силы взаимодействия? Расстояние между пузырьками
#.
240. Свинцовый шар радиуса # = 5 0 см имеет внутри
сферическую полость радиуса г = 5 см, центр которой находится
на расстоянии d=40 см от центра шара (рис. 99)
С какой силой будет притягиваться к шару материальная
точка массы >п= 10 г, находящаяся на расстоянии /=80 см
от центра шара, если линия>-соединяющая центры шара и
полости, составляет угол а =60° с линией, соединяющей
центр шара с материальной точкой?»
241. Тело, размерами которого можно пренебречь, помещено
внутрь тонкой’однородной сферы. Доказать, что
сила притяжения, действующая со стороны сферы на тело,
равна нулю при любом положенин тела внутри сферы.
53 СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ. Закон всемирного тяготения.
242, С какой силой притягивается к центру Земли тело
массы т, находящееся в глубокой шахте, если расстояние
от тела до центра Земли равно г? Плотность Земли считать
всюду одинаковой и. равной р.
54 СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ. Закон всемирного тяготения.
§ 9. Закон всемирного тяготения. Ответы.
228. По второму закону Ньютона m^g — F, где /к,-—ицертная
масса, т. е. величина, характеризующая способность тел приобретать
-то или иное ускорение под влиянием определенной силы. С другой
стороны, по закону всемирного тяготения F=ymgMg/R2, где коэффициент
пропорциональности у—так называемая гравитационная
постоянная, а mg и Mg—гравитационные массы взаимодействующих
тел. Гравитационная масса Определяет силу гравитационного притяжения
и , в этом смысле может быть названа «гравитационным зарядом
».
Заранее не очевидно, что m.i — mg. Однако лишь при выполнении
этого равенства (достаточно и пропорциональности) ускорение свобод
ного падения одинаково для всех тел, так как при подстановке силы
тяготения во второй закон Ньютона массы пц и mg можно сократить,
и g= yM /R 2. Только сила тяготения сообщает всем телам одинаковые
ускорения, не зависящие от их масс.
229. Ускорение. g — yM/R2 (см. задачу 228). Принимая g =
=9,81 м/с2, найдем у = 6,67-10-11 м3/кг-с2.
230. Тела внутри космического корабля перестанут оказывать
давление на его стенки, если они будут иметь такое же ускорение
как и корабль. Одинаковое ускорение в Данном участке простран
241 СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ. Закон всемирного тяготения.
ства всем хелвм независимо от их массы может сообщить только
сила тяготения. Следовательно, необходима, чтобы двигатель корабля
был выключен а сопротивление внешней средня отсутствовало. Движение
же корабля может происходить в любом направлении по
отношению к направлению сил тяготения.
231. Сила тяжести сообщает одинаковое ускорение маятнику и
рамке. Никаких деформаций за счет тяготения при свободном падении
в системе не возникает. Поэтому относительно рамки маятник
будет двигаться так, как если бы тяготения не было (см, решение
задачи 230). Он будет вращаться с постоянной угловой скоростью
до тех пор, пока длится падение рамки.
232. На участке ВСА (рис.’376) сила тяготения совершает положительную
работу (угол -0! острый) и, следовательно, скорость
планеты возрастает. В точке А скорость достигает своего максимального
значения. На участке ADB сила тяготения совершает отрицательную
работу (угол 02 тупой), и, следовательно, при движении по
этому участку скорость планеты убывает, достигая минимального
значения в точке В.
233. Чтобы спутник двигался по замкнутой орбите (окружности
радиуса на него должна действовать сила, направленная
к центру. Этой силой в данном случае является сила притяжения
Земли. По второму закону Ньютона
mv2/(R + ft) = ymM/(R+ A)2,
где M —масса Земли, R = 6370 км—радиус земного шара, у—гравитационная
достоянная. На поверхности Земля mg. Следовательно,
v= У gR2/(R-{-h) я 7,5 км/с.
.234. Под влиянием сопротивления атмосферы спутник постепенно
с течением времени приближается к Земле. Радиус его орбиты уменьшается.
Так как в верхних слоях сопротивление мало, то за один
оборот это уменьшение радиуса незначительно. Считая орбиту приближенно
круговой, можно записать
mzfl/R ^ymM/R*,
где R — радиус орбиты. Отсюда У уЯЩ , т. е. скорость спутника
возрастает при уменьшении R. Наглядно этот результат можно
пояснить следующим образом. Вследствие сопротивления атмосферы
движение спутника, выведенного, например, на круговую орбиту
242 СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ. Закон всемирного тяготения.
(пунктир на рис. 377), будет в действительности происходить по некоторой
спирали (сплошная линия на рис. 377). Поэтому проекция
F силы тяготения на направление скорости спутника v отлична от
нуля. Работа силы F (сила F больше силы сопротивления атмосферы
f) к привадит и увеличению скорости.
При движении в атмосфере полная механическая энергия спутника
уменьшается, но потенциальная энергия при приближении
к Земле убывает быстрее, чем полная. За счет этого кинетическая
энергию растет. Следует подчеркнуть, что в плотных слоях атмосферы
из-за большой величины силы сопротивления мы не можем
даже приближенно рассматривать движение, спутника как вращение
m окружности, а наш вывод несправедлив.
235. Если бросить контейнер против движения спутника А, то
он начнет двигаться та некоторому эллипсу 2, расположенному
внутри орбиты спутника (ряс. 378). Период обращения контейнера
будет немного меньше периода обращения спутника В. Поэтому earn
могут встретиться в точке соприкосновения орбит только после совершения
большого числа оборотов.
Контейнер нужно бросить в направлении движения спутника А.
Отяачяет двигаться по эллипсу 3. Скорость ч нужно подобрать
так, чтобы за время одного, оберега контейнера спутник В также
сделал один оборот к щпштняыеьив ирошел путь AS. Это вполне
возможно, так как период обращения по эллипсу 3 несколько больше
периода обращения по круговой орбшж /. Контейнер встретится- со
спутником в точке соприкосновения орбит 3 и /.
238. Считая приближенно орбиту Земли круговой, для силы
тяготения можно записать выражение F — maAR, где т. — масса
Земли, а ш = 2л/Т — угловая скорость Земли (Т — 365 дней). С другой
стороны, согласно закону тяготения F=ymM/R2, где М —масса
Солнца. Отсюда ■
ymMjR2 = mu>lR, или M = a>2R2jy и 2-1030 кг.
237. Поскольку как Луна, так и спутник движутся в поле тяжести
Земли, применим третий закоа Кеплера:
П /Т 1 = (h+ Н + 2Rafj8R ^
(ряс, 379). Ошада h= 2R(T1/Tip *—Н -Ж * = Ш км,
243 СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ. Закон всемирного тяготения.
238. Так как масса шарика больше массы воды в том же объеме,
то поле тяготения больше вблизи шарика, чем вдали от него. Соответственно
вода возле шарика дополнительно сжата. Сила давления
жидкости, действующая на пузырек слева, будет несколько меньше,
чем сила, действующая справа. С другой стороны, сила тяготения
между воздухом в пузырьке и шариком больше силы притяжения
между воздухом и выделенным
_—> —- пунктиром объемом воды (объем а
— _ на рис. 380). Так как масса воз- f’ * — духа в пузырьке очень мала, то
_£ решающим оказывается действие
первого фактора. Пузырек будет
отталкиваться от шарика.
Рис. 380. Движение железного шарика,
напротив, будет определяться тем,
что сила притяжения между воздухом в пузырьке и шариком много
меньше силы притяжения между шариком и выделенным пунктиром
объемом воды (рис. 380, объем Ь). Вычисление силы проводится
путем следующих рассуждений. В однородной среде (вода) имеется
сфера с почти полным отсутствием массы (пузырек) и сфера с избыточной
массой (шарик). Формально это можно рассматривать как
наличие отрицательной и положительной масс.
Сила взаимодействия между сферами в жидкости равна силе
взаимодействия в пустоте отрицательной массы, равной массе воды
в объеме пузырька, и положительной массы, равной избытку массы
железного шарика над массой воды в том же объеме. Следовательно,
F — — ymi(m2—mi)//?2. Здесь mi—масса воды в сфере радиуса г,
т а—масса железного шарика.
239. Вблизи пузырька поле тяготения меньше, чем в однородной
жидкости. Жидкость соответственно сжата здесь меньше. Поэтому
в участок жидкости возле одного пузырька устремляется другой,
и наоборот. Пузырьки будут притягиваться. Два пузырька в однородной
жидкости, массы которых пренебрежимо малы, можно рассматривать
формально как отрицательные массы, наложенные на
положительную массу т среды в объеме пузырька:
; F = y (—m)( — m)//?2 = у т 2//?2.
240. Если бы шар был сплошным, то сила тяготения F1 = yMm/li,
где М = */sitRsp —- масса шара без полости. Наличие полости экви-
валентно появлению силы отталкивания Fi = ym’m/S2, где т’ = */3л г3р,
a S—расстояние между центром полости и материальной точкой.
244 СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ. Закон всемирного тяготения.
Искомая сила F является геометрической суммой сил Рг и Ft
(рис. 381). По теореме косинусов
241. Искомая сила притяжения будет являться геометрической
суммой сил притяжения, создаваемых отдельными элементами сферы.
Малые элементы и о2 (рис. 382) вырезаются из сферы конусами
с вершиной в точке А, которые получаются при вращении образующей
ВС вокруг оси SjS2. Площади элементов равны соответственно
(j4Si)2o)/cos at и (i4S2)2o)/cos а 2, а их массы (^S 1)2(op/cos а х и
(v4S2)2a)p/cos а 2, где со—телесный угол, под которым видны оба
элемента из точки А; р — поверхностная плотность сферы (масса,
приходящаяся на единицу площади); Z a i — Z «а. так как треугольник
S]OS2 равнобедренный. Силы притяжения, создаваемые элементами,
соответственно равны
где m—масса тела, и направлены в противоположные стороны. Их
равнодействующая равна нулю.
Проводя аналогичные рассуждения для других соответствующих
элементов сферы, убеждаемся, что все они попарно компенсируют
друг друга. Следовательно, сила притяжения, которая действует со
стороны сферы на тело, помещенное внутри нее, равна нулю. Заметим,
что данный результат справедлив и для сферы конечной толщины,
так как ее можно разбить на сколь угодно тонкйЬ сферические
оболочки, для каждой из которых справедливо доказанное выше
утверждение.
242. Сила притяжения равна силе, с которой тело массы т
притягивается к шару радиуса г и плотности р. Внешние слои толщи
Земли не оказывают, как доказано в задаче 241, на тело никакого
245 СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ. Закон всемирного тяготения.
действия. Поэтому искомая сила
Эта сила убывает пропорционально г по нере приближения к центру
Земли.
246 СБОРНИК ЗАДАЧ ПО ЭЛЕМЕНТАРНОЙ ФИЗИКЕ. Закон всемирного тяготения.